题目内容
19．$\overrightarrow{a}$+$\overrightarrow{b}$+$\overrightarrow{c}$=$\overrightarrow{0}$，$\overrightarrow{a}$•$\overrightarrow{b}$=$\overrightarrow{b}$•$\overrightarrow{c}$=$\overrightarrow{c}$•$\overrightarrow{a}$=-1，则|$\overrightarrow{a}$|=$\sqrt{2}$．分析 由$\overrightarrow{a}$+$\overrightarrow{b}$+$\overrightarrow{c}$=$\overrightarrow{0}$得$\overrightarrow{c}$=-$\overrightarrow{a}-\overrightarrow{b}$，计算$\overrightarrow{a}•\overrightarrow{c}$，根据$\overrightarrow{a}$•$\overrightarrow{b}$=$\overrightarrow{b}$•$\overrightarrow{c}$=$\overrightarrow{c}$•$\overrightarrow{a}$=-1列出方程解出${\overrightarrow{a}}^{2}$．
解答 解：∵$\overrightarrow{a}$+$\overrightarrow{b}$+$\overrightarrow{c}$=$\overrightarrow{0}$，∴$\overrightarrow{c}$=-$\overrightarrow{a}-\overrightarrow{b}$．
∴$\overrightarrow{a}$•$\overrightarrow{c}$=-$\overrightarrow{a}•$（$\overrightarrow{a}+\overrightarrow{b}$）=-${\overrightarrow{a}}^{2}$-$\overrightarrow{a}•\overrightarrow{b}$．
∵$\overrightarrow{a}$•$\overrightarrow{b}$=$\overrightarrow{b}$•$\overrightarrow{c}$=$\overrightarrow{c}$•$\overrightarrow{a}$=-1，
∴-${\overrightarrow{a}}^{2}$+1=-1．∴${\overrightarrow{a}}^{2}$=2．
∴$|\overrightarrow{a}|$=$\sqrt{2}$．
故答案为：$\sqrt{2}$．
点评 本题考查了平面向量的数量积运算，属于基础题．
| A． | （$\frac{π}{2}$，π） | B． | （$\frac{π}{4}$，$\frac{3π}{4}$） | C． | （π，$\frac{3π}{2}$） | D． | （$\frac{3π}{4}$，$\frac{5π}{4}$） |
| A． | a≥0 | B． | a≥$\frac{3}{2}$ | C． | a≥$\frac{3+\sqrt{5}}{4}$ | D． | a≥$\frac{5}{4}$ |
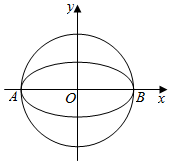如图，椭圆$W：\frac{x^2}{a^2}+\frac{y^2}{b^2}=1（a＞b＞0）$的离心率为$\frac{{\sqrt{3}}}{2}$，其左顶点A在圆O：x2+y2=16上．