题目内容
18.利用单位圆写出符合下列条件的角x的取值范围.(1)cosx$>\frac{1}{2}$;
(2)|cosx|$≤\frac{1}{2}$;
(3)sinx$≥\frac{1}{2}$且tanx≤-1.
分析 在单位圆中画出三角函数线.
(1)由[0,2π)内,cos$\frac{π}{3}$=cos$\frac{5π}{3}$=$\frac{1}{2}$,结合余弦线得cosx$>\frac{1}{2}$的解集;
(2)由[0,2π)内,cos$\frac{π}{3}$=cos$\frac{5π}{3}$=$\frac{1}{2}$,cos$\frac{2π}{3}$=cos$\frac{4π}{3}$=-$\frac{1}{2}$,结合余弦线得$-\frac{1}{2}≤$cosα$≤\frac{1}{2}$的解集.
(3)由[0,2π)内,sin$\frac{π}{6}$=sin$\frac{5π}{6}$=$\frac{1}{2}$,tan$\frac{3π}{4}$=tan$\frac{7π}{4}$=-1,结合正切线、正弦线得sinx$≥\frac{1}{2}$且tanx≤-1.的解集.
解答 解:在单位圆内作三角函数线如图:
(1)在[0,2π)内,cos$\frac{π}{3}$=cos$\frac{5π}{3}$=$\frac{1}{2}$,
满足cosx$>\frac{1}{2}$的角的终边在阴影部分内(不含边界),
∵cos$\frac{π}{3}$=cos(-$\frac{π}{3}$),
∴cosx$>\frac{1}{2}$的解集为{α|-$\frac{π}{3}$+2kπ<α<$\frac{π}{3}$+2kπ,k∈Z};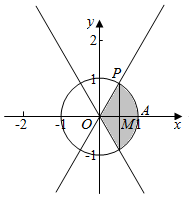
(2)由|cosx|$≤\frac{1}{2}$;得$-\frac{1}{2}$≤cosx$≤\frac{1}{2}$;
∵在[0,2π)内,cos$\frac{π}{3}$=cos$\frac{5π}{3}$=$\frac{1}{2}$,cos$\frac{2π}{3}$=cos$\frac{4π}{3}$=-$\frac{1}{2}$,
∴满足$-\frac{1}{2}$≤cosx$≤\frac{1}{2}$的终边在阴影部分内,
∴$-\frac{1}{2}$≤cosx$≤\frac{1}{2}$的解集为{α|$\frac{π}{3}$+2kπ≤α≤$\frac{2π}{3}$,或$\frac{4π}{3}$+2kπ≤α≤$\frac{5π}{3}$+2kπ,k∈Z}.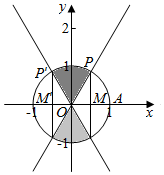
(3)∵在[0,2π)内,[0,2π)内,sin$\frac{π}{6}$=sin$\frac{5π}{6}$=$\frac{1}{2}$,tan$\frac{3π}{4}$=tan$\frac{7π}{4}$=-1,
满足sinx$≥\frac{1}{2}$的集合为α|$\frac{π}{6}$+2kπ≤α≤$\frac{5π}{6}$+2kπ,k∈Z}.
满足tanx≤-1的集合为α|-$\frac{π}{2}$+kπ<α≤$-\frac{π}{4}$+kπ,k∈Z}.
则同时满足sinx$≥\frac{1}{2}$且tanx≤-1的解集为{α|-$\frac{π}{2}$+kπ<α≤$\frac{5π}{6}$+2kπ,k∈Z}.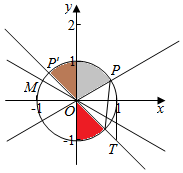
点评 本题考查了三角函数线,考查了三角不等式的解法,考查了数形结合的解题思想方法,属于基本知识的考查.

| A. | ($\frac{π}{2}$,π) | B. | ($\frac{π}{4}$,$\frac{3π}{4}$) | C. | (π,$\frac{3π}{2}$) | D. | ($\frac{3π}{4}$,$\frac{5π}{4}$) |
| A. | $\frac{21}{2}$ | B. | $\frac{15}{4}$ | C. | 10 | D. | 5 |
| A. | a≥0 | B. | a≥$\frac{3}{2}$ | C. | a≥$\frac{3+\sqrt{5}}{4}$ | D. | a≥$\frac{5}{4}$ |
