题目内容
20．若球的表面积变为原来的2倍，则半径变为原来的$\sqrt{2}$倍．分析 设原球的半径r，变化之后半径为R，结合题意由球的表面积公式可得4πR2=2×4πr2，变形可得R=$\sqrt{2}$r，即可得答案．
解答 解：设原球的半径r，变化之后半径为R，
则原球的表面积为4πr2，变化之后的表面积为4πR2，
其表面积扩大2倍，即4πR2=2×4πr2，
则R=$\sqrt{2}$r，
即半径变为原来的$\sqrt{2}$倍；
故答案为：$\sqrt{2}$．
点评 本题考查球的表面积，解题的关键是掌握球的表面积公式．
练习册系列答案
相关题目
11．
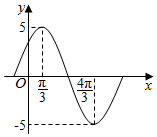已知函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，0＜φ＜π）的图象如图所示，若f（α）=3，α∈（$\frac{π}{3}$，$\frac{5π}{6}$），则sinα的值为（ ）
已知函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，0＜φ＜π）的图象如图所示，若f（α）=3，α∈（$\frac{π}{3}$，$\frac{5π}{6}$），则sinα的值为（ ）| A． | $\frac{3\sqrt{3}+4}{10}$ | B． | $\frac{3\sqrt{3}-4}{10}$ | C． | $\frac{3+4\sqrt{3}}{10}$ | D． | $\frac{3-4\sqrt{3}}{10}$ |
9．已知集合M={a|cosα＜sinα，0≤α≤2π}，N={α|tanα＜sinα}，那么M∩N是（ ）
| A． | （$\frac{π}{2}$，π） | B． | （$\frac{π}{4}$，$\frac{3π}{4}$） | C． | （π，$\frac{3π}{2}$） | D． | （$\frac{3π}{4}$，$\frac{5π}{4}$） |
10．设a＞1，x，y满足约束条件$\left\{\begin{array}{l}{y≥x}\\{y≤ax}\\{x+2y≤2}\end{array}\right.$，若目标函数z=x+ay最大值不小于$\frac{3}{2}$，则实数a的取值范围为（ ）
| A． | a≥0 | B． | a≥$\frac{3}{2}$ | C． | a≥$\frac{3+\sqrt{5}}{4}$ | D． | a≥$\frac{5}{4}$ |