题目内容
10.在锐角三角形ABC 中,角 A,B,C 的对边分别为 a,b,c.若a=2bsinC,则tanA+tanB+tanC的最小值是( )| A. | 4 | B. | $3\sqrt{3}$ | C. | 8 | D. | $6\sqrt{3}$ |
分析 由题意求得tanB+tanC=2tanBtanC ①,tanA+tanB+tanC=tanA•tanB•tanC ②,化简tanA+tanB+tanC,利用基本不等式求得它的最小值.
解答 解:在锐角三角形ABC 中,sinA=sin(B+C)=sinBcosC+cosBsinC.
∵a=2bsinC,∴sinA=2sinBsinC,∴sinBcosC+cosBsinC=2sinBsinC,
化简可得tanB+tanC=2tanBtanC ①.
∵tanA=-tan(B+C)=$\frac{tanB+tanC}{tanBtanC-1}$>0,∴tanB+tanC=tanA(tanBtanC-1),
∴tanA+tanB+tanC=tanA•tanB•tanC ②,且tanB•tanC-1>0.
则tanA+tanB+tanC=tanA•tanB•tanC=$\frac{tanB+tanC}{tanBtanC-1}$•tanBtanC,令tanB•tanC-1=m,则m>0,
故tanA+tanB+tanC=$\frac{tanB+tanC}{m}$•(m+1)=$\frac{2tanBtanC}{m}$•(m+1)=$\frac{2m+2}{m}$•(m+1)=$\frac{{2(m+1)}^{2}}{m}$=4+2m+$\frac{2}{m}$≥4+2$\sqrt{4}$=8,
当且仅当2m=$\frac{2}{m}$,即m=1时,取等号,此时,tanB•tanC=2,
故tanA+tanB+tanC的最小值是8,
故选:C.
点评 本题主要考查诱导公式,两角和差的正切公式,基本不等式的应用,属于中档题.

练习册系列答案
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目
1.已知$λ=3\int_0^1{{x^2}dx}$,在矩形ABCD中,AB=2,AD=1,点P为矩形ABCD内一点,则使得$\overrightarrow{AP}•\overrightarrow{AC}≥λ$的概率为( )
| A. | $\frac{1}{8}$ | B. | $\frac{1}{4}$ | C. | $\frac{3}{4}$ | D. | $\frac{7}{8}$ |
5.已知函数f ( x)=2ax-a+3,若?x0∈(-1,1),f ( x0 )=0,则实数 a 的取值范围是( )
| A. | (-∞,-3)∪(1,+∞) | B. | (-∞,-3) | C. | (-3,1) | D. | (1,+∞) |
2.已知α为第四象限角,$sinα+cosα=\frac{1}{5}$,则$tan\frac{α}{2}$的值为( )
| A. | $-\frac{1}{2}$ | B. | $\frac{1}{2}$ | C. | $-\frac{1}{3}$ | D. | $\frac{1}{3}$ |
19.设函数f(x)=$\left\{\begin{array}{l}3x-1,x<1\\{2}^{x},x≥1\end{array}\right.$,则满足f(f(a))=2f(a)的a取值范围是( )
| A. | [$\frac{2}{3}$,+∞) | B. | [$\frac{2}{3}$,1] | C. | [1,+∞) | D. | [0,1] |
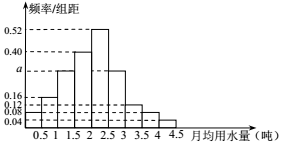 我国是世界上严重缺水的国家,城市缺水问题较为突出.某市政府为了鼓励居民节约用水,计划在本市试行居民生活用水定额管理,即确定一个合理的居民月用水量标准x(吨),用水量不超过 x 的部分按平价收费,超出 x 的部分按议价收费.为了了解全市居民用水量的分布情况,通过抽样,获得了 100 位居民某年的月均用水量(单位:吨),将数据按照[0,0.5),[0.5,1),…,[4,4.5]分成9组,制成了如图所示的频率分布直方图.
我国是世界上严重缺水的国家,城市缺水问题较为突出.某市政府为了鼓励居民节约用水,计划在本市试行居民生活用水定额管理,即确定一个合理的居民月用水量标准x(吨),用水量不超过 x 的部分按平价收费,超出 x 的部分按议价收费.为了了解全市居民用水量的分布情况,通过抽样,获得了 100 位居民某年的月均用水量(单位:吨),将数据按照[0,0.5),[0.5,1),…,[4,4.5]分成9组,制成了如图所示的频率分布直方图.