题目内容
1.已知直线ax+by+c=0(a,b,c都是正数)与圆x2+y2=2相切,则以a,b,c为三边长的三角形( )| A. | 锐角三角形 | B. | 直角三角形 | C. | 钝角三角形 | D. | 不存在 |
分析 由题意可得,圆心到直线的距离$\frac{|c|}{\sqrt{{a}^{2}+{b}^{2}}}$=$\sqrt{2}$,即 c2=2a2+2b2,故可得结论.
解答 解:∵直线ax+by+c=0(a,b,c都是正数)与圆x2+y2=2相切,
∴圆心到直线的距离 $\frac{|c|}{\sqrt{{a}^{2}+{b}^{2}}}$=$\sqrt{2}$,即 c2=2a2+2b2,
∴cosC=$\frac{{a}^{2}+{b}^{2}-{c}^{2}}{2ab}$≤-1
故以a,b,c为三边长的三角形不存在,
故选D.
点评 本题考查直线和圆的位置关系,点到直线的距离公式,得到圆心到直线的距离$\frac{|c|}{\sqrt{{a}^{2}+{b}^{2}}}$=$\sqrt{2}$,即c2=2a2+2b2是解题的关键.

练习册系列答案
相关题目
12.函数f(x)=2-$\frac{3}{x}$在区间[1,3]上的最大值是( )
| A. | 2 | B. | 3 | C. | -1 | D. | 1 |
6.如图所示的程序框图,如果输出的是30,那么判断框中应填写( )


| A. | i>3? | B. | i≤5? | C. | i<4? | D. | i≤4? |
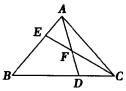 如图,在△ABC中,AE:EB=1:3,BD:DC=2:1,AD与CE相交于点F,则$\frac{EF}{FC}+\frac{AF}{FD}$的值为$\frac{3}{2}$.
如图,在△ABC中,AE:EB=1:3,BD:DC=2:1,AD与CE相交于点F,则$\frac{EF}{FC}+\frac{AF}{FD}$的值为$\frac{3}{2}$. 在棱长均相等的正三棱柱ABC-A1B1C1中,M,N,D分别是棱B1C1,C1C,BC的中点.
在棱长均相等的正三棱柱ABC-A1B1C1中,M,N,D分别是棱B1C1,C1C,BC的中点.