题目内容
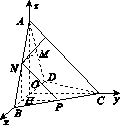
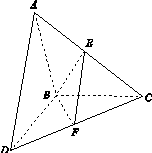
三棱锥A BCD及其侧视图、俯视图如图14所示.设M,N分别为线段AD,AB的中点,P为线段BC上的点,且MN⊥NP.
(1)证明:P是线段BC的中点;
(2)求二面角A NP M的余弦值.
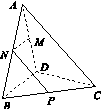
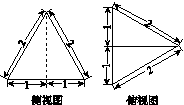
图14
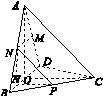
解:(1)如图所示,取BD的中点O,连接AO,CO.
由侧视图及俯视图知,△ABD,△BCD为正三角形,
所以AO⊥BD,OC⊥BD.
因为AO,OC⊂平面AOC,且AO∩OC=O,
所以BD⊥平面AOC.
又因为AC⊂平面AOC,所以BD⊥AC.
取BO的中点H,连接NH,PH.
又M,N,H分别为线段AD,AB,BO的中点,所以MN∥BD,NH∥AO,
因为AO⊥BD,所以NH⊥BD.
因为MN⊥NP,所以NP⊥BD.
因为NH,NP⊂平面NHP,且NH∩NP=N,所以BD⊥平面NHP.
又因为HP⊂平面NHP,所以BD⊥HP.
又OC⊥BD,HP⊂平面BCD,OC⊂平面BCD,所以HP∥OC.
因为H为BO的中点,所以P为BC的中点.
(2)方法一:如图所示,作NQ⊥AC于Q,连接MQ.
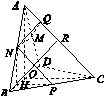
由(1)知,NP∥AC,所以NQ⊥NP.
因为MN⊥NP,所以∠MNQ为二面角A NP M的一个平面角.
由(1)知,△ABD,△BCD为边长为2的正三角形,所以AO=OC= .
.
由俯视图可知,AO⊥平面BCD.
因为OC⊂平面BCD,所以AO⊥OC,因此在等腰直角△AOC中,AC=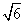 .
.
作BR⊥AC于R
因为在△ABC中,AB=BC,所以R为AC的中点,
所以BR=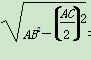 =
=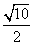 .
.
因为在平面ABC内,NQ⊥AC,BR⊥AC,
所以NQ∥BR.
又因为N为AB的中点,所以Q为AR的中点,
所以NQ=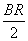 =
=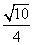 .
.
同理,可得MQ=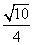 .
.
故△MNQ为等腰三角形,
所以在等腰△MNQ中,
cos∠MNQ=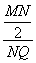 =
=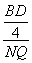 =
=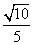 .
.
故二面角A NP M的余弦值是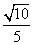 .
.
方法二:由俯视图及(1)可知,AO⊥平面BCD.
因为OC,OB⊂平面BCD,所以AO⊥OC,AO⊥OB.
又OC⊥OB,所以直线OA,OB,OC两两垂直.
如图所示,以O为坐标原点,以OB,OC,OA的方向为x轴,y轴,z轴的正方向,建立空间直角坐标系O xyz.
则A(0,0, ),B(1,0,0),C(0,
),B(1,0,0),C(0, ,0),D(-1,0,0).
,0),D(-1,0,0).
因为M,N分别为线段AD,AB的中点,
又由(1)知,P为线段BC的中点,
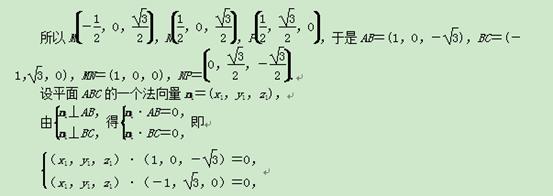
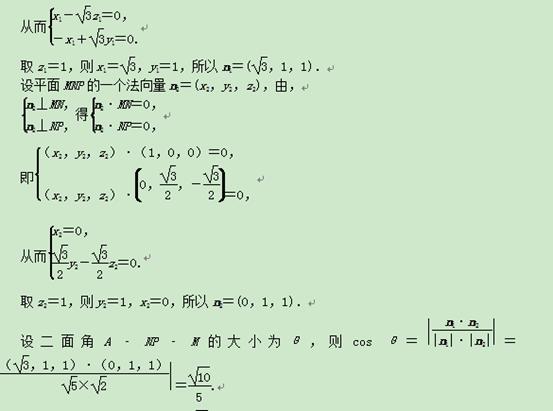 故二面角ANPM的余弦值是
故二面角ANPM的余弦值是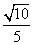 .
.

 ).若S1,S2,S3分别是三棱锥D ABC在xOy,yOz,zOx坐标平面上的正投影图形的面积,则( )
).若S1,S2,S3分别是三棱锥D ABC在xOy,yOz,zOx坐标平面上的正投影图形的面积,则( ) DC,F为EC的中点.现将△DAE沿AE翻折到△PAE的位置,如图J112②所示,且平面PAE⊥平面ABCE.
DC,F为EC的中点.现将△DAE沿AE翻折到△PAE的位置,如图J112②所示,且平面PAE⊥平面ABCE.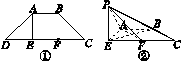
 B.
B.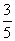
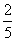 D.
D.