题目内容
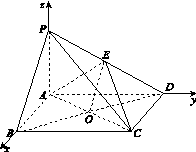
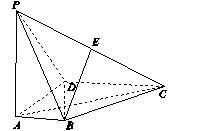
如图13,四棱锥PABCD中,底面ABCD为矩形,PA⊥平面ABCD,E为PD的中点.
(1)证明:PB∥平面AEC;
(2)设二面角DAEC为60°,AP=1,AD= ,求三棱锥EACD的体积.
,求三棱锥EACD的体积.
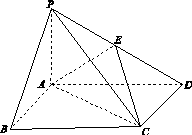
图13
解:(1)证明:连接BD交AC于点O,连接EO.
因为ABCD为矩形,所以O为BD的中点.
又E为PD的中点,所以EO∥PB.
因为EO⊂平面AEC,PB⊄平面AEC,
所以PB∥平面AEC.
(2)因为PA⊥平面ABCD,ABCD为矩形,
所以AB,AD,AP两两垂直.
如图,以A为坐标原点, ,AD,AP的方向为x轴、y轴、z轴的正方向,|
,AD,AP的方向为x轴、y轴、z轴的正方向,| |为单位长,建立空间直角坐标系Axyz,则D
|为单位长,建立空间直角坐标系Axyz,则D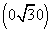 ,E
,E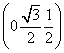 ,
,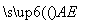 =
=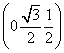 .
.
设B(m,0,0)(m>0),则C(m, ,0),
,0),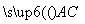 =(m,
=(m, ,0).
,0).
设n1=(x,y,z)为平面ACE的法向量,
则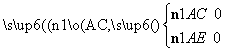 即
即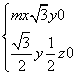
可取n1=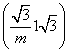 .
.
又n2=(1,0,0)为平面DAE的法向量,
由题设易知|cos〈n1,n2〉|= ,即
,即
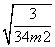 =
= ,解得m=
,解得m=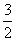 .
.
因为E为PD的中点,所以三棱锥EACD的高为 .三棱锥EACD的体积V=
.三棱锥EACD的体积V=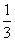 ×
× ×
× ×
×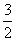 ×
× =
=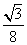 .
.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目

 B.
B.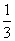
 D.
D.