题目内容
cos
= .
| 2π |
| 3 |
考点:运用诱导公式化简求值
专题:三角函数的求值
分析:应用诱导公式化简三角函数式,可得结果.
解答:
解:cos
=cos(π-
)=-cos
=-
,
故答案为:-
| 2π |
| 3 |
| π |
| 3 |
| π |
| 3 |
| 1 |
| 2 |
故答案为:-
| 1 |
| 2 |
点评:本题主要考查应用诱导公式化简三角函数式,要特别注意符号的选取,这是解题的易错点,属于基础题.

练习册系列答案
相关题目
如果双曲线的a=2,一个焦点为(5,0),则其标准方程为( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
若存在对于定义域为R的函数f(x),若存在非零实数x0,使函数f(x)在(-∞,x0)和(x0,+∞)上均有零点,则称x0为函数f(x)的一个“纽点”.则下列四个函数中,不存在“纽点”的是( )
| A、f(x)=x2+bx-1(b∈R) | ||
| B、f(x)=2x-x2 | ||
C、f(x)=
| ||
| D、f(x)=2-|x-1| |
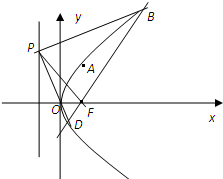 在平面直角坐标系xOy中,抛物线C的顶点在原点,经过点A(1,2)其焦点F在x轴上.
在平面直角坐标系xOy中,抛物线C的顶点在原点,经过点A(1,2)其焦点F在x轴上.