题目内容
给出下列命题:
①若p+q>m+n,则一定有p>m或q>n;
②若a>0,b>0,且
+
=1,则ab≥4;
③曲线y=x2和曲线y2=x围成的图形面积是
;
④设随机变量ξ服从正态分布N(0,1),若P(ξ>1)=P,则P(-1<ξ<0)=
-P.
正确命题的个数是( )
①若p+q>m+n,则一定有p>m或q>n;
②若a>0,b>0,且
| 2 |
| a |
| 1 |
| b |
③曲线y=x2和曲线y2=x围成的图形面积是
| 1 |
| 3 |
④设随机变量ξ服从正态分布N(0,1),若P(ξ>1)=P,则P(-1<ξ<0)=
| 1 |
| 2 |
正确命题的个数是( )
| A、1 | B、2 | C、3 | D、4 |
考点:命题的真假判断与应用
专题:阅读型,不等式的解法及应用,概率与统计
分析:①可通过假设p≤m且q≤n,由不等式的性质,即可推出矛盾,从而得到①正确;
②直接运用基本不等式,即可求出ab的范围;
③画出图,运用定积分∫
(
-x2)dx,求出即得面积;
④根据正态分布的特点:正态曲线关于x=0对称,以及概率的特点,即可求出P(-1<ξ<0).
②直接运用基本不等式,即可求出ab的范围;
③画出图,运用定积分∫
1 0 |
| x |
④根据正态分布的特点:正态曲线关于x=0对称,以及概率的特点,即可求出P(-1<ξ<0).
解答:
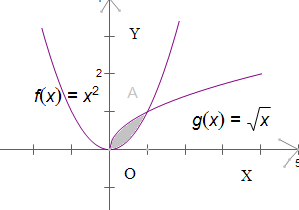 解:①假设p≤m且q≤n,则p+q≤m+n,
解:①假设p≤m且q≤n,则p+q≤m+n,
这与p+q>m+n矛盾,故①正确;
②若a>0,b>0,且
+
=1,
由
+
≥2
,得ab≥8,故②错;
③曲线y=x2和曲线y2=x围成的图形如右图,
由
解得
或
,即A(1,1),
故所求面积为∫
(
-x2)dx=(
x
-
x3)|
=
-
=
,故③正确;
④由于随机变量ξ服从标准正态分布N(0,1),则正态曲线关于x=0对称,由P(ξ>1)=p,
则P(1>ξ>0)=
-p,故P(-1<ξ<0)=
-p,故④正确.
故选C.
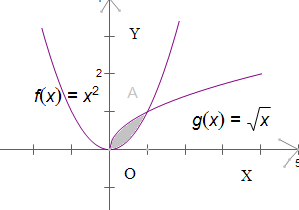 解:①假设p≤m且q≤n,则p+q≤m+n,
解:①假设p≤m且q≤n,则p+q≤m+n,这与p+q>m+n矛盾,故①正确;
②若a>0,b>0,且
| 2 |
| a |
| 1 |
| b |
由
| 2 |
| a |
| 1 |
| b |
|
③曲线y=x2和曲线y2=x围成的图形如右图,
由
|
|
|
故所求面积为∫
1 0 |
| x |
| 2 |
| 3 |
| 3 |
| 2 |
| 1 |
| 3 |
1 0 |
=
| 2 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
④由于随机变量ξ服从标准正态分布N(0,1),则正态曲线关于x=0对称,由P(ξ>1)=p,
则P(1>ξ>0)=
| 1 |
| 2 |
| 1 |
| 2 |
故选C.
点评:本题以命题的真假为载体,考查不等式的性质及基本不等式的应用,定积分的运用,正态分布的特点及概率的计算,属于基础题.

练习册系列答案
相关题目
函数y=x-ln(1+x)的单调递增区间为( )
| A、(-1,0) |
| B、(-∞,-1)和(0,+∞) |
| C、(0,+∞) |
| D、(-∞,-1) |
某学校高一、高二、高三年级的学生人数分别为900、900、1200人,现用分层抽样的方法从该校高中三个年级的学生中抽取容量为50的样本,则应从高三年级抽取的学生人数为( )
| A、15 | B、20 | C、25 | D、30 |
函数f(x)=lnx+2x-6的零点属于区间(n,n+1)(n∈z),则n等于( )
| A、1 | B、2 | C、3 | D、4 |
在△ABC中,tanA=-1,C=30°,BC=2
,则AB等于( )
| 2 |
| A、4 | B、3 | C、2 | D、1 |
对于?a>1,b>1,以下不等式不成立的是( )
| A、logab>0 | ||||
| B、ab>1 | ||||
C、(
| ||||
| D、logab+logba≥2 |
已知函数f(x)=(x2-2x)ex,x∈[-2,+∞),f′(x)是函数f(x)的导函数,且f′(x)有两个零点x1和x2(x1<x2),则f(x)的最小值为( )
| A、f(x1) |
| B、f(x2) |
| C、f(-2) |
| D、以上都不对 |