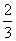题目内容
已知定义在R上的函数y=f(x)满足以下三个条件:①对于任意的x∈R,都有f(x+1)=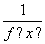 ;②函数y=f(x+1)的图象关于y轴对称;③对于任意的x1,x2∈[0,1],且x1<x2,都有f(x1)>f(x2),则f
;②函数y=f(x+1)的图象关于y轴对称;③对于任意的x1,x2∈[0,1],且x1<x2,都有f(x1)>f(x2),则f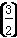 ,f(2),f(3)从小到大的关系是________.
,f(2),f(3)从小到大的关系是________.
f(3)<f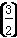 <f(2)
<f(2)
[解析] 由①得f(x+2)=f(x+1+1)= =f(x),所以函数f(x)的周期为2.
=f(x),所以函数f(x)的周期为2.
因为函数y=f(x+1)的图象关于y轴对称,将函数y=f(x+1)的图象向右平移一个单位即得y=f(x)的图象,所以函数y=f(x)的图象关于x=1对称;根据③可知函数f(x)在[0,1]上为减函数,又结合②知,函数f(x)在[1,2]上为增函数.
因为f(3)=f(2+1)=f(1),在区间[1,2]上,1< <2,
<2,
所以f(1)<f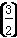 <f(2),
<f(2),
即f(3)<f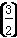 <f(2).
<f(2).

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
 ,AC=2,BC=1,M,N分别是AC、PB的中点.
,AC=2,BC=1,M,N分别是AC、PB的中点. (Ⅰ)求证:BC⊥PA;
(Ⅰ)求证:BC⊥PA; ln(1-x)的定义域是( )
ln(1-x)的定义域是( ) 的图象可能是( )
的图象可能是( )


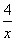 是定义在集合M=
是定义在集合M=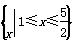 上的两个函数.对任意的x∈M,存在常数x0∈M,使得f(x)≥f(x0),g(x)≥g(x0),且f(x0)=g(x0).则函数f(x)在集合M上的最大值为( )
上的两个函数.对任意的x∈M,存在常数x0∈M,使得f(x)≥f(x0),g(x)≥g(x0),且f(x0)=g(x0).则函数f(x)在集合M上的最大值为( )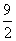 B.4
B.4 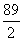
 的平面点集中随机取一点M(x0,y0),设事件A=“y0<2x0”,那么事件A发生的概率是( )
的平面点集中随机取一点M(x0,y0),设事件A=“y0<2x0”,那么事件A发生的概率是( )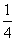 B.
B.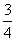 C.
C.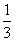 D.
D.