题目内容
已知f(x)=2x2+px+q,g(x)=x+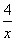 是定义在集合M=
是定义在集合M=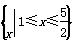 上的两个函数.对任意的x∈M,存在常数x0∈M,使得f(x)≥f(x0),g(x)≥g(x0),且f(x0)=g(x0).则函数f(x)在集合M上的最大值为( )
上的两个函数.对任意的x∈M,存在常数x0∈M,使得f(x)≥f(x0),g(x)≥g(x0),且f(x0)=g(x0).则函数f(x)在集合M上的最大值为( )
A.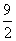 B.4
B.4
C.6 D.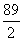
C
[解析] 函数g(x)=x+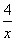 在区间
在区间 上的最小值为4,最大值为5,对任意的x∈M,存在常数x0∈M,使得g(x)≥g(x0),则g(x0)=g(x)min=4,此时x0=2,根据题意知,f(x)min=f(2)=4,即二次函数f(x)=2x2+px+q的顶点坐标为(2,4),因此-
上的最小值为4,最大值为5,对任意的x∈M,存在常数x0∈M,使得g(x)≥g(x0),则g(x0)=g(x)min=4,此时x0=2,根据题意知,f(x)min=f(2)=4,即二次函数f(x)=2x2+px+q的顶点坐标为(2,4),因此- =2,p=-8,f(2)=2×22-2×8+q=q-8=4,q=12,
=2,p=-8,f(2)=2×22-2×8+q=q-8=4,q=12,
∴f(x)=2x2-8x+12=2(x-2)2+4,因此函数f(x)在集合M上的最大值为f(x)max=f(1)=6,故选C.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案已知函数f(x)=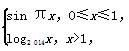
若a,b,c互不相等,且f(a)=f(b)=f(c),则a+b+c的取值范围是( )
A.(1,2 014) B.(1,2 015)
C.(2,2 015) D.[2,2 015]
生产A,B两种元件,其质量按测试指标划分为:指标大于或等于82为正品,小于82为次品,现随机抽取这两种元件各100件进行检测,检测结果统计如下:
| 测试指标 | [70,76) | [76,82) | [82,88) | [88,94) | [94,100] |
| 元件A | 8 | 12 | 40 | 32 | 8 |
| 元件B | 7 | 18 | 40 | 29 | 6 |
(1)试分别估计元件A、元件B为正品的概率;
(2)生产一件元件A,若是正品可盈利50元,若是次品则亏损10元;生产一件元件B,若是正品可盈利100元,若是次品则亏损20元,在(1)的前提下:
①求生产5件元件B所获得的利润不少于300元的概率;
②记X为生产1件元件A和1件元件B所得的总利润,求随机变量X的分布列和数学期望.
 ≤a(x+2y)恒成立,则实数a的最小值为( )
≤a(x+2y)恒成立,则实数a的最小值为( )
 a2;
a2; ;②函数y=f(x+1)的图象关于y轴对称;③对于任意的x1,x2∈[0,1],且x1<x2,都有f(x1)>f(x2),则f
;②函数y=f(x+1)的图象关于y轴对称;③对于任意的x1,x2∈[0,1],且x1<x2,都有f(x1)>f(x2),则f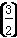 ,f(2),f(3)从小到大的关系是________.
,f(2),f(3)从小到大的关系是________.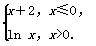 若函数y=|f(x)|-k(x+e2)的零点恰有四个,则实数k的值为( )
若函数y=|f(x)|-k(x+e2)的零点恰有四个,则实数k的值为( )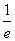

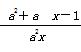 (a≠0)是1型函数,则n-m的最大值为
(a≠0)是1型函数,则n-m的最大值为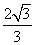 ;
;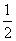 x2+x是3型函数,则m=-4,n=0;
x2+x是3型函数,则m=-4,n=0;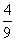 .
.