题目内容
已知正△PAB与△ABC所在平面垂直,且AB= ,AC=2,BC=1,M,N分别是AC、PB的中点.
,AC=2,BC=1,M,N分别是AC、PB的中点.
 (Ⅰ)求证:BC⊥PA;
(Ⅰ)求证:BC⊥PA;
(Ⅱ)求异面直线MN与PA所成的角;
解:(Ⅰ)∵AB= ,AC=2,BC=1,∴AB2+ BC2 =AC2,
,AC=2,BC=1,∴AB2+ BC2 =AC2,
∴ BC⊥AB ……………… 3分
又∵面PAB⊥面ABC,交线为AB,BCÌ面ABC
 ∴BC⊥平面PAB. …………………… 6分
∴BC⊥平面PAB. …………………… 6分
∴BC⊥PA. …………………………… 7分
(Ⅱ)取AB中点O,连接MO,NO,
∵N是PB的中点,∴NO∥PA,
∴∠MNO为异面直线MN与PA所成的角.
∵MO∥BC,由(Ⅰ)可得MO⊥平面PAB.
在直角三角形MNO中,MO= ,NO=
,NO= ,
,
∴ ,
, ,
,
∴异面直线MN与PA所成的角为 .
.

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
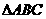 中,
中,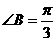 ,三边长a,b,c成等差数列,且
,三边长a,b,c成等差数列,且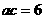 ,则b的值是
,则b的值是 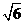 B.
B.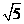 C.
C.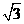 D.
D.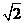
 的值是 .
的值是 . 若z=kx+y的最大值为13,则实数k=( )
若z=kx+y的最大值为13,则实数k=( ) C.
C. D.5
D.5 ≤a(x+2y)恒成立,则实数a的最小值为( )
≤a(x+2y)恒成立,则实数a的最小值为( )
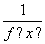 ;②函数y=f(x+1)的图象关于y轴对称;③对于任意的x1,x2∈[0,1],且x1<x2,都有f(x1)>f(x2),则f
;②函数y=f(x+1)的图象关于y轴对称;③对于任意的x1,x2∈[0,1],且x1<x2,都有f(x1)>f(x2),则f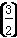 ,f(2),f(3)从小到大的关系是________.
,f(2),f(3)从小到大的关系是________.