题目内容
函数f(n)＝logn＋1(n＋2)(n∈N*)，定义使f(1)·f(2)·f(3)·…·f(k)为整数的数k(k∈N*)叫做企盼数，则在区间[1,2 013]内这样的企盼数共有________个．
9
[解析] ∵logn＋1(n＋2)＝
，
∴f(1)·f(2)·f(3)·…·f(k)＝
·
·
·…·
＝
＝log2(k＋2)．
∵1 024＝210,2 048＝211，且log24＝2，
∴在区间[1,2 013]内使f(1)·f(2)·f(3)·…·f(k)为整数的数有10－1＝9个．
练习册系列答案
阅读快车系列答案
相关题目
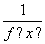；②函数y＝f(x＋1)的图象关于y轴对称；③对于任意的x1，x2∈[0,1]，且x1<x2，都有f(x1)>f(x2)，则f
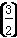，f(2)，f(3)从小到大的关系是________．
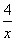不可能是k型函数；
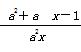(a≠0)是1型函数，则n－m的最大值为
；
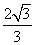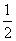x2＋x是3型函数，则m＝－4，n＝0；
.
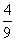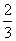＋4(a，b∈R)，若f
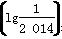＝2 013，则f(lg 2 014)＝( )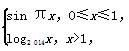
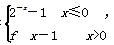若方程f(x)＝x＋a有且只有两个不相等的实数根，则实数a的取值范围为( )