题目内容
设p：函数f(x)＝2|x－a|在区间(4，＋∞)上单调递增；q：loga2<1.如果“非p”是真命题，“p或q”也是真命题，那么实数a的取值范围是________．
(4，＋∞)
[解析] ∵“非p”为真命题，∴p为假命题，又p或q为真命题，∴q为真命题．
若a>1，由loga2<1知a>2，又f(x)＝2|x－a|在(a，＋∞)上单调递增，且p为假命题，∴a>4，因此得，a>4；
若0<a<1，则p、q都是真命题，不合题意．
综上，a的取值范围是(4，＋∞)．
练习册系列答案
相关题目
则
是这个数列的（ ）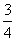
}，N＝{x|n－
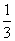≤x≤n}，且M，N都是集合{x|0≤x≤1}的子集，如果把b－a叫做集合{x|a≤x≤b}的“长度”，那么集合M∩N的“长度”的最小值是( )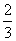
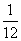D.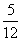
>
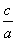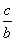”的逆否命题是真命题；
＝1表示椭圆”的________条件．