题目内容
给出下列命题：
①任意实数α，sinα=
成立；
②函数y=tan（2x+
）的最小正周期为π；
③x=
是函数y=sin（2x+
）的图象的一条对称轴方程；
④存在实数α，β，使sin（α-β）=sinα-sinβ成立．
其中正确的命题是 ．（填上所有正确的序号）
①任意实数α，sinα=
| 1-cos2α |
②函数y=tan（2x+
| π |
| 3 |
③x=
| π |
| 8 |
| π |
| 4 |
④存在实数α，β，使sin（α-β）=sinα-sinβ成立．
其中正确的命题是
考点：命题的真假判断与应用
专题：计算题,简易逻辑
分析：利用同角三角函数关系、三角函数的对称性、两角和与差的公式，即可得出结论．
解答：
解：①任意实数α，sinα=
或sinα=-
，故不正确；
②函数y=tan（2x+
）的最小正周期为
，故不正确；
③x=
时，y=sin（2x+
）取得最大值，∴x=
是函数y=sin（2x+
）的图象的一条对称轴方程，故正确；
④存在实数β=0，使sin（α-β）=sinα-sinβ成立，故正确．
故答案为：③④．
| 1-cos2α |
| 1-cos2α |
②函数y=tan（2x+
| π |
| 3 |
| π |
| 2 |
③x=
| π |
| 8 |
| π |
| 4 |
| π |
| 8 |
| π |
| 4 |
④存在实数β=0，使sin（α-β）=sinα-sinβ成立，故正确．
故答案为：③④．
点评：本题主要考查同角三角函数关系、两角和与差的公式和三角函数的对称性．考查三角函数公式的综合应用．三角函数的公式比较多，很容易记混，平时要注意积累．是基础题
练习册系列答案
学而优衔接教材南京大学出版社系列答案
相关题目
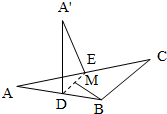在直角△ABC中，AB=BC=2，D，E分别是AB，AC的中点，将△ADE沿线段DE折起到△A′DE，使平面A′DE⊥平面DBCE，当M是DE的中点时，证明：BM⊥面A′CD．