题目内容
2.已知函数$f(x)=\left\{\begin{array}{l}2-|x|,x≤2\\{({x-2})^2},x>2\end{array}\right.$,函数$g(x)=\frac{b}{2}-f(2-x)$,其中b∈R,若函数y=f(x)-g(x)恰有4个零点,则b的取值范围是( )| A. | $(\frac{7}{8},+∞)$ | B. | $(\frac{7}{4},2)$ | C. | $(\frac{7}{8},1)$ | D. | $(\frac{7}{2},4)$ |
分析 求出函数y=f(x)-g(x)的表达式,构造函数h(x)=f(x)+f(2-x),作出函数h(x)的图象,利用数形结合进行求解即可.
解答 解:∵g(x)=$\frac{b}{2}$-f(2-x),
∴y=f(x)-g(x)=f(x)-$\frac{b}{2}$+f(2-x),
由f(x)-$\frac{b}{2}$+f(2-x)=0,得f(x)+f(2-x)=$\frac{b}{2}$,
设h(x)=f(x)+f(2-x),
若x≤0,则-x≥0,2-x≥2,
则h(x)=f(x)+f(2-x)=2+x+x2,
若0≤x≤2,则-2≤-x≤0,0≤2-x≤2,
则h(x)=f(x)+f(2-x)=2-x+2-|2-x|=2-x+2-2+x=2,
若x>2,-x<-2,2-x<0,
则h(x)=f(x)+f(2-x)=(x-2)2+2-|2-x|=x2-5x+8.
作出函数h(x)的图象如图: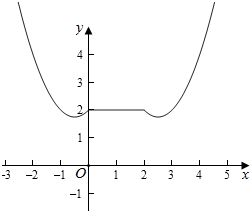
当x≤0时,h(x)=2+x+x2=(x+$\frac{1}{2}$)2+$\frac{7}{4}$≥$\frac{7}{4}$,
当x>2时,h(x)=x2-5x+8=(x-$\frac{5}{2}$)2+$\frac{7}{4}$≥$\frac{7}{4}$,
故当$\frac{b}{2}$=$\frac{7}{4}$时,h(x)=$\frac{b}{2}$,有两个交点,
当$\frac{b}{2}$=2时,h(x)=$\frac{b}{2}$,有无数个交点,
由图象知要使函数y=f(x)-g(x)恰有4个零点,
即h(x)=$\frac{b}{2}$恰有4个根,
则满足$\frac{7}{4}$<$\frac{b}{2}$<2,解得:b∈($\frac{7}{2}$,4),
故选:D.
点评 本题主要考查函数零点个数的判断,根据条件求出函数的解析式,利用数形结合是解决本题的关键.

 如图,矩形ABCD中AD边的长为1,AB边的长为2,矩形ABCD位于第一象限,且顶点A,D分别在x轴y轴的正半轴上(含原点)滑动,则$\overrightarrow{OB}$$•\overrightarrow{OC}$的最大值是( )
如图,矩形ABCD中AD边的长为1,AB边的长为2,矩形ABCD位于第一象限,且顶点A,D分别在x轴y轴的正半轴上(含原点)滑动,则$\overrightarrow{OB}$$•\overrightarrow{OC}$的最大值是( )| A. | $\sqrt{5}$ | B. | 5 | C. | 6 | D. | 7 |
| A. | K的最小值为1 | B. | K的最大值为1 | C. | K的最小值为$2\sqrt{2}$ | D. | K的最大值为$2\sqrt{2}$ |
| A. | $-\frac{5}{2}$ | B. | 0 | C. | $\frac{5}{3}$ | D. | $\frac{5}{2}$ |
| 商店名称 | A | B | C | D | E |
| 销售额x(千万元) | 3 | 5 | 6 | 7 | 9 |
| 利润额y(百万元) | 2 | 3 | 3 | 4 | 5 |
| A. | 2.3 | B. | 3.2 | C. | 4.2 | D. | 2.4 |