题目内容
1,4,9,16…这些数可以用图1的点阵表示,古希腊毕达哥拉斯学派将其称为正方形数,记第n个数为an+1,在图2的杨辉三角中,第n(n≥2)行是(a+b)n-1展开式的二项式系数
,
,…,
记杨辉三角的前n行所有数之和为Tn.
(Ⅰ)求an和Tn的通项公式;
(Ⅱ)当n≥2时,比较an与Tn的大小,并加以证明.
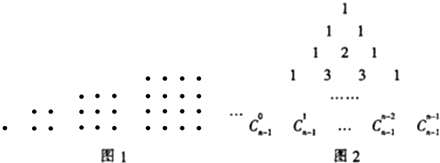
| C | 0 n-1 |
| C | 1 n-1 |
| C | n-1 n-1 |
(Ⅰ)求an和Tn的通项公式;
(Ⅱ)当n≥2时,比较an与Tn的大小,并加以证明.
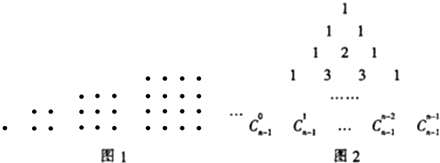
考点:数列的求和,归纳推理
专题:等差数列与等比数列
分析:(Ⅰ)由正方形数的特点知an=n2,由二项式定理的性质,求出杨辉三角形第n行n个数的和,由此能求出an和Tn的通项公式.
(Ⅱ)2≤n≤4时,an>Tn.n≥5时,an<Tn.证明:2≤n≤4时,an>Tn时,可以逐个验证;证明n≥5时,an<Tn时,可以用数学归纳法证明.
(Ⅱ)2≤n≤4时,an>Tn.n≥5时,an<Tn.证明:2≤n≤4时,an>Tn时,可以逐个验证;证明n≥5时,an<Tn时,可以用数学归纳法证明.
解答:
解:(Ⅰ)由正方形数的特点知an=n2,
由二项式定理的性质,杨辉三角形第n行n个数的和为:
Sn
+
=2n-1,
∴Tn=S1+S2+…+Sn
=1+2+22+…+2n-1
=2n-1.
(Ⅱ)a2=4,T2=22-1=3,∴a2>T2.
a3=9,T3=23-1=7,∴a3>T3.
a4=16,T4=24-1=15,∴a4>T4.
a5=25,T5=25-1=31,∴a5<T5.
∴2≤n≤4时,an>Tn.
猜想2≤n≤4时,an>Tn.n≥5时,an<Tn.
证明:2≤n≤4时,an>Tn,已证明.
下面用数学归纳法证明n≥5时,an<Tn.
①当n=5时,a5=25,T5=25-1=31,∴a5<T5.成立.
②假设n=k(k≥5,k∈N*)时,猜想成立,即ak<2k,∴k2<2k-1.
则Tk+1=2k+1-1=2•2k-1
=2(2k-1)+1
>2k2+1=k2+k2+1
>k2+2k+1=(k+1)2,
∴n=k+1时,猜想也成立.
由①②知n≥5时,an<Tn.
由二项式定理的性质,杨辉三角形第n行n个数的和为:
Sn
| =C | 0 n-1 |
| +C | 1 n-1 |
| C | n-1 n-1 |
∴Tn=S1+S2+…+Sn
=1+2+22+…+2n-1
=2n-1.
(Ⅱ)a2=4,T2=22-1=3,∴a2>T2.
a3=9,T3=23-1=7,∴a3>T3.
a4=16,T4=24-1=15,∴a4>T4.
a5=25,T5=25-1=31,∴a5<T5.
∴2≤n≤4时,an>Tn.
猜想2≤n≤4时,an>Tn.n≥5时,an<Tn.
证明:2≤n≤4时,an>Tn,已证明.
下面用数学归纳法证明n≥5时,an<Tn.
①当n=5时,a5=25,T5=25-1=31,∴a5<T5.成立.
②假设n=k(k≥5,k∈N*)时,猜想成立,即ak<2k,∴k2<2k-1.
则Tk+1=2k+1-1=2•2k-1
=2(2k-1)+1
>2k2+1=k2+k2+1
>k2+2k+1=(k+1)2,
∴n=k+1时,猜想也成立.
由①②知n≥5时,an<Tn.
点评:本题考查数列的通项公式的求法,考查不等式的证明,解题时要认真审题,注意二项式定理和数学归纳法的合理运用.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
函数f(a)=(3m-1)a+b-2m,当m∈[0,1]时,0≤f(a)≤1恒成立,则
的最大值是( )
| b2-a2 |
| ab |
A、
| ||
| B、4 | ||
C、
| ||
| D、5 |
已知y=f(x)满足xf′(x)>-f(x)在R上恒成立,且a>b,则( )
| A、af(b)>bf(a) |
| B、af(a)>bf(b) |
| C、af(a)<bf(b) |
| D、af(b)<bf(a) |