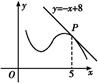
题目内容
设函数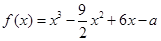 .
.
(1)对于任意实数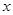 ,
,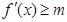 恒成立,求
恒成立,求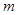 的最大值;
的最大值;
(2)若方程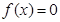 有且仅有一个实根,求
有且仅有一个实根,求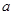 的取值范围.
的取值范围.
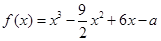 .
.(1)对于任意实数
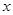 ,
,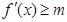 恒成立,求
恒成立,求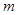 的最大值;
的最大值;(2)若方程
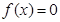 有且仅有一个实根,求
有且仅有一个实根,求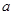 的取值范围.
的取值范围.(1) (2)
(2) 或
或
 (2)
(2) 或
或
试题分析:(1)先求导,因为
 为二次函数,所以对于任意实数
为二次函数,所以对于任意实数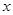 ,
,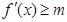 恒成立,即
恒成立,即 恒成立。所以此二次函数的图像应开口向上,判别式小于等于0。(2)分别解
恒成立。所以此二次函数的图像应开口向上,判别式小于等于0。(2)分别解 得函数
得函数 的单调性和极值。画图分析可知要使
的单调性和极值。画图分析可知要使 只有一个根则应极大值小于0或极小值大于0.
只有一个根则应极大值小于0或极小值大于0.试题解析:解:(1)
 , 2分
, 2分因为
 ,
, , 即
, 即  恒成立, 4分
恒成立, 4分所以
 , 得
, 得 ,
,即
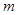 的最大值为
的最大值为 6分
6分(2) 因为 当
 时,
时,  ;当
;当 时,
时,  ;
;当
 时,
时,  ; 8分
; 8分所以 当
 时,
时, 取极大值
取极大值  ;
;当
 时,
时, 取极小值
取极小值  ; 10分
; 10分故当
 或
或 时, 方程
时, 方程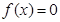 仅有一个实根.
仅有一个实根. 解得
 或
或 . 14分
. 14分
练习册系列答案
相关题目
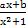 在点(-1,f(-1))处的切线方程为x+y+3=0.
在点(-1,f(-1))处的切线方程为x+y+3=0.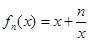 ,(
,(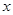 >0,
>0,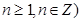 ,以点
,以点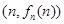 为切点作函数
为切点作函数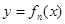 图象的切线
图象的切线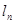 ,记函数
,记函数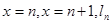 所围成的区域面积为
所围成的区域面积为 .
.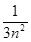 ;
;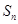 为数列
为数列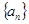 的前
的前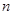 项和,求证:
项和,求证: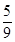 .来
.来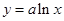
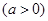 在
在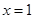 处的切线与两坐标轴围成的三角形的面积为4,则
处的切线与两坐标轴围成的三角形的面积为4,则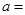 .
.