题目内容
2.已知f(x)为偶函数,且当x≥0时,f(x)=x(1+x),则满足f(x)≤2的x的取值范围是[-1,1].分析 可令x(1+x)=2,根据x≥0从而解得x=1,根据二次函数的单调性容易判断f(x)在[0,+∞)上单调递增,这样便可由f(x)≤2得到f(|x|)≤f(1),根据f(x)在[0,+∞)上单调递增便可得出|x|≤1,从而便可得出满足f(x)≤2的x的取值范围.
解答 解:令x(1+x)=2,解得x=1,或-2(舍去);
x≥0时,f(x)=x2+x,对称轴为x=$-\frac{1}{2}$,在[0,+∞)上单调递增;
∵f(x)为偶函数;
∴由f(x)≤2得,f(|x|)≤f(1);
∴|x|≤1;
∴-1≤x≤1;
∴满足f(x)≤2的x的取值范围是[-1,1].
故答案为:[-1,1].
点评 考查一元二次方程的解法,二次函数的单调性,增函数的定义,以及偶函数的定义,绝对值不等式的解法.

练习册系列答案
 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案
相关题目
10.为了得到函数y=sin x+cos x的图象,可以将函数y=$\sqrt{2}$sinx的图象( )
| A. | 向右平移$\frac{π}{12}$个单位 | B. | 向右平移$\frac{π}{4}$个单位 | ||
| C. | 向左平移$\frac{π}{12}$个单位 | D. | 向左平移$\frac{π}{4}$个单位 |
7.已知等差数列{an}的前n项和为Sn,a1+a5=0,且a9=20.则S11=( )
| A. | 260 | B. | 220 | C. | 130 | D. | 110 |
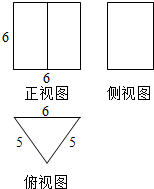 某几何体的三视图如图所示,其中正视图是边长为6的正方形,俯视图是腰长为5,底边长为6的等腰三角形,则该几何体的体积是72,表面积是120.
某几何体的三视图如图所示,其中正视图是边长为6的正方形,俯视图是腰长为5,底边长为6的等腰三角形,则该几何体的体积是72,表面积是120. 如图,一辆汽车在一条水平的公路上向正西行驶,到A处时测的公路北侧一山顶D在西偏北30°的方向上,行驶1200m后到达B处,测得此山顶D在西偏北75°的方向上,仰角为60°,则此山的高度CD=600$\sqrt{6}$m.
如图,一辆汽车在一条水平的公路上向正西行驶,到A处时测的公路北侧一山顶D在西偏北30°的方向上,行驶1200m后到达B处,测得此山顶D在西偏北75°的方向上,仰角为60°,则此山的高度CD=600$\sqrt{6}$m.