题目内容
7.已知圆M与直线3x-4y=0及3x-4y+10=0都相切,圆心在直线y=-x-4上,则圆M的标准方程为(x+3)2+(y+1)2=1.分析 首先根据题意设圆心坐标为(a,-a-4),再由直线与圆相切利用圆心到直线的距离为半径,求出a和半径r,即可得到圆的方程.
解答 解:∵圆心在直线y=-x-4上,
∴设圆心坐标为(a,-a-4),
∵圆M与直线3x-4y=0相切
∴圆心(a,-a-4)到两直线3x-4y=0的距离为:$\frac{|3a-4(-a-4)|}{\sqrt{{3}^{2}+{4}^{2}}}$=r,即$\frac{|7a+16|}{5}$=r ①
同理圆心(a,-a-4)到两直线3x-4y+10=0的距离为:$\frac{|3a-4(-a-4)+10|}{\sqrt{{3}^{2}+{4}^{2}}}$=r,即$\frac{|7a+26|}{5}$=r ②
联立①②得,a=-3,r2=1.
∴圆M的方程为:(x+3)2+(y+1)2=1.
故答案为:(x+3)2+(y+1)2=1.
点评 本题考查了圆的标准方程,直线与圆相切以及点到直线的距离公式,一般情况下:求圆C的方程,就是求圆心、求半径.

练习册系列答案
 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
17.x>0是$\frac{1}{x}$-1>0成立的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
15.《九章算术》中记载了公元前344年商鞅督造的一种标准量器--商鞅同方升,其主体部分的三视图如图所示,则该量器的容积为( )
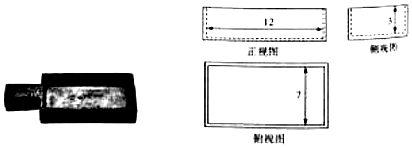

| A. | 252 | B. | 189 | C. | 126 | D. | 63 |
2.若cos($\frac{π}{8}$-α)=$\frac{1}{5}$,则cos($\frac{3π}{4}$+2α)的值为( )
| A. | $\frac{23}{25}$ | B. | -$\frac{23}{25}$ | C. | $\frac{7}{8}$ | D. | -$\frac{7}{8}$ |