题目内容
3．
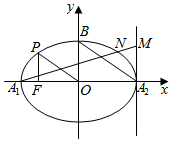如图，椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的左右顶点分别为A1，A2，上顶点为B，从椭圆上一点P向x轴作垂线，垂足恰为左焦点F，且A2B∥OP，|FA2|=$\sqrt{10}$+$\sqrt{5}$，过A2作x轴的垂线l，点M是l上任意一点，A1M交椭圆于点N，则$\overrightarrow{OM}$•$\overrightarrow{ON}$=（ ）| A． | 10 | B． | 5 | ||
| C． | 15 | D． | 随点M在直线l上的位置变化而变化 |
分析 由F的坐标，求得P的坐标，运用两直线平行的条件：斜率相等，可得b=c，再由条件可得a=$\sqrt{10}$，b=c=$\sqrt{5}$，求得椭圆方程，设出M的坐标，设出直线MN的方程，联立椭圆方程，消去y，由韦达定理可得N的横坐标，进而得到N的纵坐标，再由向量的数量积的坐标表示，计算即可得到所求值．
解答 解：由F（-c，0），可得P（-c，$\frac{{b}^{2}}{a}$），
A2（a，0），B（0，b），即有kOP=${k}_{{A}_{2}B}$，
可得-$\frac{{b}^{2}}{ac}$=-$\frac{b}{a}$，即有b=c，a=$\sqrt{2}$c，
|FA2|=a+c=$\sqrt{10}$+$\sqrt{5}$，
解得a=$\sqrt{10}$，b=c=$\sqrt{5}$，
即有椭圆的方程为$\frac{{x}^{2}}{10}$+$\frac{{y}^{2}}{5}$=1，
设M（$\sqrt{10}$，t），A1（-$\sqrt{10}$，0），
即有直线A1M：y=$\frac{t}{2\sqrt{10}}$（x+$\sqrt{10}$），
代入椭圆方程x2+2y2=10，
可得（20+t2）x2+2$\sqrt{10}$t2x+10t2-200=0，
（-$\sqrt{10}$）•xN=$\frac{10{t}^{2}-200}{20+{t}^{2}}$，
可得xN=$\frac{（20-{t}^{2}）\sqrt{10}}{20+{t}^{2}}$，
yN=$\frac{t}{2\sqrt{10}}$（xN+$\sqrt{10}$）=$\frac{20t}{20+{t}^{2}}$，
则$\overrightarrow{OM}$•$\overrightarrow{ON}$=$\sqrt{10}$•$\frac{（20-{t}^{2}）\sqrt{10}}{20+{t}^{2}}$+t•$\frac{20t}{20+{t}^{2}}$
=$\frac{200+10t}{20+{t}^{2}}$=10．
故选：A．
点评 本题考查向量的数量积的坐标表示，考查椭圆的方程和性质，以及直线的方程的运用，以及联立直线和椭圆方程，运用韦达定理，考查化简整理的运算能力，属于中档题．
初中暑期衔接系列答案
| A． | [$\frac{\sqrt{3}}{2}$，1） | B． | [$\frac{\sqrt{2}}{2}$，$\frac{\sqrt{3}}{2}$] | C． | [$\frac{\sqrt{2}}{2}$，1） | D． | [$\frac{1}{2}$，1） |
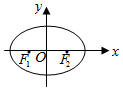平面直角坐标系xOy中，已知F1、F2分别是椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的左、右焦点，且右焦点F2的坐标为（$\sqrt{3}$，0），点（$\sqrt{3}$，$\frac{1}{2}$）在椭圆C上．