题目内容
14.下列命题:①奇函数f(x)必满足f(0)=0;
②函数f(x)=loga(3x-2)+1的图象过定点(1,1)
③A=R+,B=R,$f:x→y=\frac{1}{x+1}$,则f为A到B的映射;
④在同一坐标系中,y=2x与y=-2-x的图象关于原点O对称.
其中真命题的序号是②③④(把你认为正确的命题的序号都填上).
分析 ①根据奇函数的定义举一个反例.
②根据对数函数过定点的性质进行求解.
③根据映射的定义进行判断.
④根据指数函数的对称性进行判断.
解答 解:①函数f(x)=$\frac{1}{x}$是奇函数f(x),但不满足f(0)=0;故①错误,
②由3x-2=1,得x=1,此时f(1)=loga1+1=0+1=1,即函数f(x)的图象过定点(1,1),故②正确,
③A=R+,B=R,$f:x→y=\frac{1}{x+1}$,则f为A到B的映射成立,故③正确,
④在同一坐标系中,y=2x与y=-2-x的图象关于原点O对称.正确,故④正确,
故答案为:②③④
点评 本题主要考查命题的真假判断,涉及函数的图象和性质,涉及的知识点较多,难度不大.

练习册系列答案
相关题目
2.设函数f(x)=$\left\{\begin{array}{l}1+lg(2-x),x<1\\{10^{x-1}},x≥1\end{array}$,则f(-98)+f(lg30)=( )
| A. | 5 | B. | 6 | C. | 9 | D. | 22 |
9.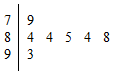 如图,是2007年在广州举行的全国少数民族运动会上,七位评委为某民族舞蹈打出的分数的茎叶统计图,去掉一个最高分和一个最低分后,所剩数据的平均数和方差分别为( )
如图,是2007年在广州举行的全国少数民族运动会上,七位评委为某民族舞蹈打出的分数的茎叶统计图,去掉一个最高分和一个最低分后,所剩数据的平均数和方差分别为( )
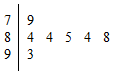 如图,是2007年在广州举行的全国少数民族运动会上,七位评委为某民族舞蹈打出的分数的茎叶统计图,去掉一个最高分和一个最低分后,所剩数据的平均数和方差分别为( )
如图,是2007年在广州举行的全国少数民族运动会上,七位评委为某民族舞蹈打出的分数的茎叶统计图,去掉一个最高分和一个最低分后,所剩数据的平均数和方差分别为( )| A. | 84,4.84 | B. | 84,1.6 | C. | 85,2.4 | D. | 85,1.6 |
3.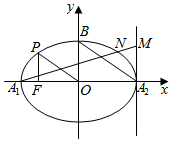 如图,椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左右顶点分别为A1,A2,上顶点为B,从椭圆上一点P向x轴作垂线,垂足恰为左焦点F,且A2B∥OP,|FA2|=$\sqrt{10}$+$\sqrt{5}$,过A2作x轴的垂线l,点M是l上任意一点,A1M交椭圆于点N,则$\overrightarrow{OM}$•$\overrightarrow{ON}$=( )
如图,椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左右顶点分别为A1,A2,上顶点为B,从椭圆上一点P向x轴作垂线,垂足恰为左焦点F,且A2B∥OP,|FA2|=$\sqrt{10}$+$\sqrt{5}$,过A2作x轴的垂线l,点M是l上任意一点,A1M交椭圆于点N,则$\overrightarrow{OM}$•$\overrightarrow{ON}$=( )
 如图,椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左右顶点分别为A1,A2,上顶点为B,从椭圆上一点P向x轴作垂线,垂足恰为左焦点F,且A2B∥OP,|FA2|=$\sqrt{10}$+$\sqrt{5}$,过A2作x轴的垂线l,点M是l上任意一点,A1M交椭圆于点N,则$\overrightarrow{OM}$•$\overrightarrow{ON}$=( )
如图,椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左右顶点分别为A1,A2,上顶点为B,从椭圆上一点P向x轴作垂线,垂足恰为左焦点F,且A2B∥OP,|FA2|=$\sqrt{10}$+$\sqrt{5}$,过A2作x轴的垂线l,点M是l上任意一点,A1M交椭圆于点N,则$\overrightarrow{OM}$•$\overrightarrow{ON}$=( )| A. | 10 | B. | 5 | ||
| C. | 15 | D. | 随点M在直线l上的位置变化而变化 |
4.某校的一个社会实践调查小组,在对该校学生的良好“用眼习惯”的调查中,随机发放了120分问卷.对收回的100份有效问卷进行统计,得到如2×2下列联表:
(1)现按女生是否能做到科学用眼进行分层,从45份女生问卷中抽取了6份问卷,从这6份问卷中再随机抽取3份,并记其中能做到科学用眼的问卷的份数X,试求随机变量X的分布列和数学期望;
(2)若在犯错误的概率不超过P的前提下认为良好“用眼习惯”与性别有关,那么根据临界值表,最精确的P的值应为多少?请说明理由.
附:独立性检验统计量${K^2}=\frac{{n{{(ad-bc)}^2}}}{(a+b)(c+d)(a+c)(b+d)}$,其中n=a+b+c+d.
独立性检验临界值表:
| 做不到科学用眼 | 能做到科学用眼 | 合计 | |
| 男 | 45 | 10 | 55 |
| 女 | 30 | 15 | 45 |
| 合计 | 75 | 25 | 100 |
(2)若在犯错误的概率不超过P的前提下认为良好“用眼习惯”与性别有关,那么根据临界值表,最精确的P的值应为多少?请说明理由.
附:独立性检验统计量${K^2}=\frac{{n{{(ad-bc)}^2}}}{(a+b)(c+d)(a+c)(b+d)}$,其中n=a+b+c+d.
独立性检验临界值表:
| P(K2≥k0) | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
| k0 | 1.323 | 2.072 | 2.706 | 3.840 | 5.024 |
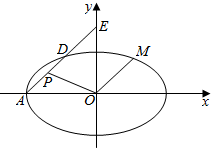 如图,在平面直角坐标系xoy中,已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的离心率e=$\frac{1}{2}$,左顶点为A(-4,0),过点A作斜率为k(k≠0)的直线l交椭圆C于点D,交y轴于点E.
如图,在平面直角坐标系xoy中,已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的离心率e=$\frac{1}{2}$,左顶点为A(-4,0),过点A作斜率为k(k≠0)的直线l交椭圆C于点D,交y轴于点E. 如图所示,O为坐标原点,过点P(4,0)且斜率为k的直线l交抛物线y2=4x于M(x1,y1),N(x2,y2)两点.
如图所示,O为坐标原点,过点P(4,0)且斜率为k的直线l交抛物线y2=4x于M(x1,y1),N(x2,y2)两点.