题目内容
11.若角α终边经过点P(-3a,5a)(a≠0),则sinα的值为±$\frac{5\sqrt{34}}{34}$.分析 根据角α的终边经过点P(-3a,5a)(a≠0),故x=-3a,y=5a,r=$\sqrt{34}$|a|,由sinα=$\frac{y}{r}$运算求得结果.
解答 解:由于角α终边经过点P(-3a,5a)(a≠0),故x=-3a,y=5a,∴r=$\sqrt{34}$|a|,
∴sinα=$\frac{y}{r}$=±$\frac{5\sqrt{34}}{34}$,
故答案为:±$\frac{5\sqrt{34}}{34}$.
点评 本题考查任意角的三角函数的定义,两点间的距离公式的应用,求出r=$\sqrt{34}$|a|是解题的关键.

练习册系列答案
相关题目
2.设函数f(x)=$\left\{\begin{array}{l}1+lg(2-x),x<1\\{10^{x-1}},x≥1\end{array}$,则f(-98)+f(lg30)=( )
| A. | 5 | B. | 6 | C. | 9 | D. | 22 |
3.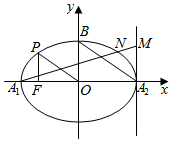 如图,椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左右顶点分别为A1,A2,上顶点为B,从椭圆上一点P向x轴作垂线,垂足恰为左焦点F,且A2B∥OP,|FA2|=$\sqrt{10}$+$\sqrt{5}$,过A2作x轴的垂线l,点M是l上任意一点,A1M交椭圆于点N,则$\overrightarrow{OM}$•$\overrightarrow{ON}$=( )
如图,椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左右顶点分别为A1,A2,上顶点为B,从椭圆上一点P向x轴作垂线,垂足恰为左焦点F,且A2B∥OP,|FA2|=$\sqrt{10}$+$\sqrt{5}$,过A2作x轴的垂线l,点M是l上任意一点,A1M交椭圆于点N,则$\overrightarrow{OM}$•$\overrightarrow{ON}$=( )
 如图,椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左右顶点分别为A1,A2,上顶点为B,从椭圆上一点P向x轴作垂线,垂足恰为左焦点F,且A2B∥OP,|FA2|=$\sqrt{10}$+$\sqrt{5}$,过A2作x轴的垂线l,点M是l上任意一点,A1M交椭圆于点N,则$\overrightarrow{OM}$•$\overrightarrow{ON}$=( )
如图,椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左右顶点分别为A1,A2,上顶点为B,从椭圆上一点P向x轴作垂线,垂足恰为左焦点F,且A2B∥OP,|FA2|=$\sqrt{10}$+$\sqrt{5}$,过A2作x轴的垂线l,点M是l上任意一点,A1M交椭圆于点N,则$\overrightarrow{OM}$•$\overrightarrow{ON}$=( )| A. | 10 | B. | 5 | ||
| C. | 15 | D. | 随点M在直线l上的位置变化而变化 |
20.已知点M(-$\sqrt{3}$,0),N($\sqrt{3}$,0),若椭圆C:$\frac{{x}^{2}}{a}$+y2=1存在点P使|PM|-|PN|=2$\sqrt{2}$,则椭圆C的离心率的取值范围是( )
| A. | (0,1) | B. | (0,$\frac{\sqrt{2}}{2}$] | C. | [$\frac{\sqrt{2}}{2}$,1) | D. | ($\frac{1}{2}$,$\frac{2}{3}$] |
 如图所示,O为坐标原点,过点P(4,0)且斜率为k的直线l交抛物线y2=4x于M(x1,y1),N(x2,y2)两点.
如图所示,O为坐标原点,过点P(4,0)且斜率为k的直线l交抛物线y2=4x于M(x1,y1),N(x2,y2)两点.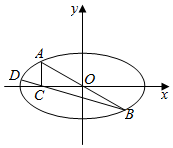 设椭圆M:$\frac{{x}^{2}}{2{c}^{2}}$+$\frac{{y}^{2}}{{c}^{2}}$=1,其中c>0.
设椭圆M:$\frac{{x}^{2}}{2{c}^{2}}$+$\frac{{y}^{2}}{{c}^{2}}$=1,其中c>0.