题目内容
图中的三个直角三角形是一个体积为2cm3的几何体的三视图,则b= cm.
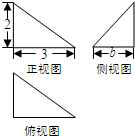

考点:由三视图求面积、体积
专题:空间位置关系与距离
分析:几何体是一个三棱锥,三棱锥的底面是一个直角三角形,两条直角边的长度分别是3,b,三棱锥的高是2,体积是2cm3,列出方程,求出b.
解答:
解:由三视图知几何体是一个三棱锥,
三棱锥的底面是一个直角三角形,两条直角边的长度分别是3,b,
三棱锥的高是2,
体积是2cm3,
∴2=
×
×3×b×2,
∴b=2,
故答案为:2
三棱锥的底面是一个直角三角形,两条直角边的长度分别是3,b,
三棱锥的高是2,
体积是2cm3,
∴2=
| 1 |
| 3 |
| 1 |
| 2 |
∴b=2,
故答案为:2
点评:本题考查由三视图还原几何体,本题解题的关键是求出几何体各个部分的长度,本题是已知体积求高,利用方程思想.

练习册系列答案
相关题目
在三角形ABC中,bcosC=CcosB,则三角形△ABC为( )
| A、等腰直角三角形 |
| B、等腰三角形 |
| C、等边三角形 |
| D、直角三角形 |

 传说古希腊毕达哥拉斯学派的数学家经常在沙滩上面画点或用小石子表示数.他们研究过如图所示的三角形数:将三角形数1,3,6,10,…记为数列{an},将可被5整除的三角形数按从小到大的顺序组成一个新数列{bn},可以推测:
传说古希腊毕达哥拉斯学派的数学家经常在沙滩上面画点或用小石子表示数.他们研究过如图所示的三角形数:将三角形数1,3,6,10,…记为数列{an},将可被5整除的三角形数按从小到大的顺序组成一个新数列{bn},可以推测: