题目内容
16.已知函数f(x)=$\frac{{λ•{2^x}+(λ-2)}}{{{2^x}+1}}$.(1)是否存在实数λ,使f(x)为奇函数.
(2)判断函数f(x)的单调性,并用单调性定义证明.
分析 (1)利用奇函数的定义,或f(0)=0,即可得出结论;
(2)根据单调性的证明步骤,即可证明结论.
解答 解:由题:f(x)=$\frac{{λ•{2^x}+(λ-2)}}{{{2^x}+1}}$=$\frac{{λ({2^x}+1)-2}}{{{2^x}+1}}$=λ$-\frac{2}{{{2^x}+1}}$.
(1)法一:∵f(x)为奇函数,∴f(-x)=-f(x)
∴λ$-\frac{2}{{{2^{-x}}+1}}$=-λ+$\frac{2}{{{2^x}+1}}$.
∴2λ=$\frac{2}{{{2^x}+1}}$+$\frac{2}{{{2^{-x}}+1}}$=$\frac{2}{{{2^x}+1}}$+$\frac{{2•{2^x}}}{{{2^x}+1}}$=$\frac{{2({2^x}+1)}}{{{2^x}+1}}$=2.
∴λ=1.
经检验 当λ=1时,f(x)为奇函数.
∴存在λ=1,使f(x)为奇函数.
法二:若存在实数λ,使f(x)为奇函数,则f(0)=0,即λ$-\frac{2}{{{2^0}+1}}$=0
∴λ=1.
当λ=1时,f(x)=1$-\frac{2}{{{2^x}+1}}$,定义域R关于原点对称
且f(x)+f(-x)=(1$-\frac{2}{{{2^x}+1}}$)+(1$-\frac{2}{{{2^{-x}}+1}}$)
=2$-\frac{2}{{{2^x}+1}}$$-\frac{{2•{2^x}}}{{{2^x}+1}}$=$2-\frac{{2({2^x}+1)}}{{{2^x}+1}}=0$
∴存在λ=1,使f(x)为奇函数.
(2)f(x)是增函数,证明如下:
设x1,x2∈且 x1<x2,则
f(x1)-f(x2)=(λ$-\frac{2}{{{2^{x_1}}+1}}$)-(λ$-\frac{2}{{{2^{x_2}}+1}}$)=$\frac{{2({2^{x_1}}-{2^{x_2}})}}{{({2^{x_1}}+1)({2^{x_2}}+1)}}$
由x1<x2可知:0<${2^{x_1}}$<${2^{x_2}}$,∴${2^{x_1}}$-${2^{x_2}}$<0,又${2^{x_1}}$+1>0,${2^{x_2}}$+1>0.
∴f(x1)-f(x2)<0,即f(x1)<f(x2).
∴λ∈R,f(x)是定义域上增函数.
点评 本题考查奇函数、单调性的定义,考查学生分析解决问题的能力,属于中档题.

| A. | $\frac{25}{6}$ | B. | $\frac{25}{8}$ | C. | $\frac{25}{3}$ | D. | $\frac{25}{4}$ |
| A. | 等腰三角形 | B. | 直角三角形 | C. | 锐角三角形 | D. | 钝角三角形 |
| A. | y轴对称 | B. | 原点对称 | C. | 直线y=x对称 | D. | 直线y=-x对称 |
| A. | (-∞,-1)∪(0,1) | B. | (-1,0)∪(1,+∞) | C. | (-1,0)∪(0,1) | D. | (-∞,-1)∪(1,+∞) |
| A. | l∥α | B. | l?α | C. | l与α相交 | D. | l?α或l与α相交 |
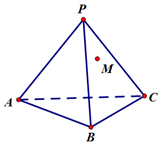 如图,正三棱锥P-ABC,已知AB=2,PA=3
如图,正三棱锥P-ABC,已知AB=2,PA=3