题目内容
已知函数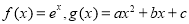 。
。
(1)若f(x)的图象与g(x)的图象所在两条曲线的一个公共点在y轴上,且在该点处两条曲线的切线互相垂直,求b和c的值。
(2)若a=c=1,b=0,试比较f(x)与g(x)的大小,并说明理由;
(3)若b=c=0,证明:对任意给定的正数a,总存在正数m,使得当x 时,
时,
恒有f(x)>g(x)成立。
(1) (2)当
(2)当 时,
时, ;当
;当 时,
时,  ;当
;当 时,
时,  .(3)详见解析
.(3)详见解析
【解析】
试题分析:(1)由题意得 ,
, ,即
,即 (2)构造函数
(2)构造函数 则
则 .当
.当 时,
时, ,
, ,
,
当 时,设
时,设 ,则
,则 ,当
,当 时,
时,  取得极小值, 且极小值为
取得极小值, 且极小值为 ,故
,故 在
在 上单调递增,
上单调递增,  ,
, (3)构造函数
(3)构造函数 ,则
,则 ,故
,故 在
在 上有最小值,
上有最小值, ,①若
,①若 ,存在
,存在 ,使当
,使当 时,恒有
时,恒有 ;若
;若 ,存在
,存在 ,使当
,使当 时,恒有
时,恒有 ;③若
;③若 ,存在
,存在 ,使当
,使当 时,恒有
时,恒有 ;
;
试题解析:(1)解:  ,
, ,
, ,
,  ,
, ,
, 2分
2分
依题意:
 ,所以
,所以
 ; 4分
; 4分
(2)解:  ,
, 时,
时, , 5分
, 5分
① 时,
时, ,
, ,即
,即
② 时,
时, ,
, ,即
,即
③ 时,令
时,令 ,则
,则 .
.
设 ,则
,则 ,
,
当 时,
时,  单调递减;当
单调递减;当 时,
时,  单调递增.
单调递增.
所以当 时,
时,  取得极小值, 且极小值为
取得极小值, 且极小值为
即 恒成立,故
恒成立,故 在
在 上单调递增,又
上单调递增,又 ,
,
因此,当 时,
时,  ,即
,即 . 9分
. 9分
综上,当 时,
时, ;当
;当 时,
时,  ;当
;当 时,
时,  . 10分
. 10分
 (3)
(3)
证法一:①若 ,由(2)知,当
,由(2)知,当 时,
时,  .即
.即 ,
,
所以, 时,取
时,取 ,即有当
,即有当 ,恒有
,恒有 .
.
②若 ,
, 即
即 ,等价于
,等价于 即
即
令 ,则
,则 .当
.当 时,
时, 在
在 内单调递增.
内单调递增.
取 ,则
,则 ,所以
,所以 在
在 内单调递增.
内单调递增.
又

即存在 ,当
,当 时,恒有
时,恒有 . 15分
. 15分
综上,对任意给定的正数 ,总存在正数
,总存在正数 ,使得当
,使得当 ,恒有
,恒有 . 16分
. 16分
证法二:设 ,则
,则 ,
,
当 时,
时, ,
, 单调减,当
单调减,当 时,
时, ,
, 单调增,
单调增,
故 在
在 上有最小值,
上有最小值, , 12分
, 12分
①若 ,则
,则 在
在 上恒成立,
上恒成立,
即当 时,存在
时,存在 ,使当
,使当 时,恒有
时,恒有 ;
;
②若 ,存在
,存在 ,使当
,使当 时,恒有
时,恒有 ;
;
③若 ,同证明一的②, 15分
,同证明一的②, 15分
综上可得,对任意给定的正数 ,总存在
,总存在 ,当
,当 时,恒有
时,恒有 . 16分
. 16分
考点:导数几何意义,利用导数研究不等式
考点分析: 考点1:导数在研究函数中的应用 考点2:函数的单调性与导数 试题属性- 题型:
- 难度:
- 考核:
- 年级:

 ,求b,c.
,求b,c. ,则
,则 则
则 _________________.
_________________. 满足
满足 ,则到x轴的距离
,则到x轴的距离 的点P的概率是 .
的点P的概率是 . .
. 的导函数为
的导函数为 ,求
,求 上的单调区间;
上的单调区间; 的极大值和极小值恰好各有一个,求实数a的取值范围.
的极大值和极小值恰好各有一个,求实数a的取值范围. 部分图象如图所示。
部分图象如图所示。
 的解析式;
的解析式; 时,求函数
时,求函数 的值域。
的值域。 ,则
,则 =
=
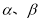 是两个相交平面,则在下列命题中,真命题的序号为 .(写出所有真命题的序号)
是两个相交平面,则在下列命题中,真命题的序号为 .(写出所有真命题的序号)  ,则在平面
,则在平面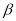 内,一定不存在与直线
内,一定不存在与直线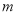 平行的直线.
平行的直线.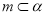 ,则在平面
,则在平面 中,
中,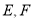 分别是
分别是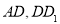 中点.
中点.
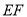 ∥平面
∥平面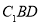 ;
;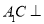 平面
平面