题目内容
如图,在正方体 中,
中,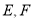 分别是
分别是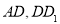 中点.
中点.

求证:(1)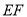 ∥平面
∥平面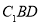 ;
;
(2)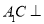 平面
平面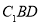 .
.
(1)详见解析(2)详见解析
【解析】
试题分析:
(1)利用正方体的性质和三角形中位线性质可得EF∥AD1,进而利用平行四边形ABC1D1转化为EF∥BC1,最后利用线面平行的判定定理证得结论.
(2)首先利用侧棱垂直于底面得到AA1⊥BD,然后结合正方形性质有AC⊥BD即可证得BD⊥平面AA1C,同理可证A1C⊥BC1最后利用线面垂直的判定定理即得结论.
试题解析:

证明:(1)连结A1D,
∵ E,F分别是AD和DD1的中点,∴ EF∥AD1 . 2分
∵ 正方体ABCD-A1B1C1D1,
∴ AB∥D1C1,AB=D1C1.
∴ 四边形ABC1D1为平行四边形,即有A1D∥BC1 4分
∴ EF∥BC1.
又EF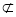 平面C1BD,BC1
平面C1BD,BC1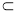 平面C1BD,
平面C1BD,
∴ EF∥平面AB1D1. 7分
(2)连结AC,则AC⊥BD.
∵ 正方体ABCD-A1B1C1D1,∴AA1⊥平面ABCD,
∴ AA1⊥BD.
又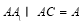 ,∴BD⊥平面AA1C,
,∴BD⊥平面AA1C,
∴ A1C⊥BD. 11分
同理可证A1C⊥BC1.
又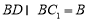 ,∴A1C⊥平面C1BD. 14分
,∴A1C⊥平面C1BD. 14分
考点:线面平行的判定定理,线面垂直的判定定理
考点分析: 考点1:点、线、面之间的位置关系 试题属性- 题型:
- 难度:
- 考核:
- 年级:

练习册系列答案
 全能测控一本好卷系列答案
全能测控一本好卷系列答案
相关题目
 。
。 时,
时,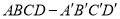 中,
中,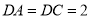 ,
,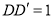 ,
,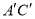 与
与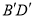 相交于点
相交于点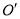 ,点
,点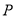 在线段
在线段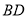 上(点
上(点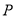 与点
与点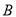 不重合).
不重合).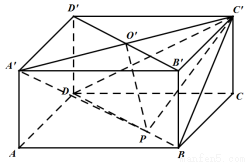
 与
与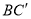 所成角的余弦值为
所成角的余弦值为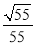 ,求
,求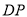 的长度;
的长度;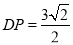 ,求平面
,求平面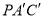 与平面
与平面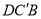 所成角的正弦值.
所成角的正弦值. 中,
中, ,
, ,则数列的前
,则数列的前 项和为 .
项和为 . ,
, ,则
,则 .
. 中,已知
中,已知 ,点
,点 分别在边
分别在边 上,且
上,且 ,点
,点 为
为 中点,则
中点,则 的值为 .
的值为 .
 在
在 上有最大值
上有最大值 ;
; 在
在 上是减函数;
上是减函数; ,使函数
,使函数 为奇函数;
为奇函数; ,
, ,满足
,满足 ”
”