题目内容

已知sinα=2cosα，则
sinα+cosα
sinα-cosα
的值是
 
．
考点：同角三角函数基本关系的运用
专题：三角函数的求值
分析：将已知等式代入原式计算即可得到结果．
解答： 解：∵sinα=2cosα，
∴原式=
2cosα+cosα
2cosα-cosα
=3．
故答案为：3
点评：此题考查了同角三角函数基本关系的运用，熟练掌握基本关系是解本题的关键．
练习册系列答案
相关题目
已知一扇形的圆心角为α，所在圆的半径为R．
（1）若α=60°，R=10cm，求扇形的弧长及扇形面积；
（2）若扇形的周长为8cm，当α为多少弧度时，该扇形有最大的面积？
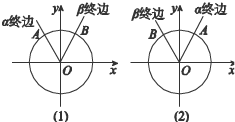如图，在平面直角坐标系xOy内作单位圆O，以Ox为始边作任意角α，β，它们的终边与单位圆O的交点分别为A，B，
（1）设α=105°，β=75°，求
OA
•
OB
；
（2）试证明两角差的余弦公式C（α-β）；cos（α-β）=cosαcosβ+sinαsinβ．
设函数f（θ）=
3
sinθ+cosθ，其中，角θ的顶点与坐标原点重合，始边与x轴非负半轴重合，终边经过点P（x，y），且0≤θ≤π．
（1）若点P的坐标为（
3
2
，
1
2
），求f（θ）的值；
（2）求满足条件的θ，使f（θ）=2．
已知函数f（x）=
ex-ax2
1+x
．
（1）若a=0，讨论f（x）的单调性．
（2）若f（x）有三个极值点x1，x2，x3．
①求a的取值范围；
②求证：x1+x2+x3＞-2．
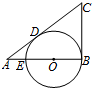如图，已知在△ABC中，∠B=90°，O是AB上一点，以O为圆心，OB为半径的圆与AB交于点E，与AC切于点D，AD=2，AE=1，则BC的长为
 
．
不等式4-x2≤0的解集为
 
．
i为虚数单位，则复数（1-2i）（1+i）的虚部是
 
．
在△ABC中，角A，B，C所对的边分别为a，b，c，已知A=
π
4
，cosB-cos2B=0，a2+c2=b-ac+2，则b=
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网