题目内容
计算下列积分
(1)∫
dx
(2)∫
(cos
-sin
)2dx.
(1)∫
1 -1 |
| 1-x2 |
(2)∫
0 |
| x |
| 2 |
| x |
| 2 |
考点:定积分
专题:导数的综合应用
分析:根据积分的几何意义和积分公式分别进行计算即可得到结论.
解答:
解:(1)∫
dx的大小等于半径为1的圆面积的
,即∫
dx=
×π×12=
.
(2)∫
(cos
-sin
)2dx=∫
(1-sinx)dx=(x+cosx)|
=
-1.
1 -1 |
| 1-x2 |
| 1 |
| 2 |
1 -1 |
| 1-x2 |
| 1 |
| 2 |
| π |
| 2 |
(2)∫
0 |
| x |
| 2 |
| x |
| 2 |
0 |
0 |
| π |
| 2 |
点评:本题主要考查积分的计算,要求熟练掌握常见函数的积分公式,对应比较复杂的积分函数要转化为求出对应曲线的面积进行求解.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
 利用如图所示算法在平面直角坐标系上打印一系列点,则打印的点在圆x2+y2=10内的共有( )个.
利用如图所示算法在平面直角坐标系上打印一系列点,则打印的点在圆x2+y2=10内的共有( )个.| A、2 | B、3 | C、4 | D、5 |
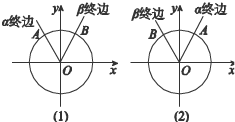 如图,在平面直角坐标系xOy内作单位圆O,以Ox为始边作任意角α,β,它们的终边与单位圆O的交点分别为A,B,
如图,在平面直角坐标系xOy内作单位圆O,以Ox为始边作任意角α,β,它们的终边与单位圆O的交点分别为A,B,