题目内容
10.已知定义在R上的奇函数f(x),对任意的实数x都有f(1+x)=f(1-x),且f(-1)=2,则f(4)+f(5)=-2.分析 求出f(0)=0,f(x)是以4为周期的周期函数,即可求出f(4)+f(5)的值.
解答 解:因为f(x)是奇函数,所以f(-x)=-f(x),f(0)=0,
又f(1+x)=f(1-x),所以f(x+2)=f(-x)=-f(x),
所以f(x+4)=f(x),即f(x)是以4为周期的周期函数,
所以f(4)+f(5)=f(0)+f(1)=f(0)-f(-1)=0-2=-2.
故答案为-2.
点评 本题考查函数的奇偶性、周期性,考查学生的计算能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
16.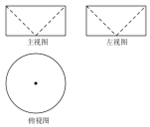 如图是一个几何体挖去另一个几何体所得的三视图,若主视图中长方形的长为2,宽为1,则该几何体的表面积为( )
如图是一个几何体挖去另一个几何体所得的三视图,若主视图中长方形的长为2,宽为1,则该几何体的表面积为( )
 如图是一个几何体挖去另一个几何体所得的三视图,若主视图中长方形的长为2,宽为1,则该几何体的表面积为( )
如图是一个几何体挖去另一个几何体所得的三视图,若主视图中长方形的长为2,宽为1,则该几何体的表面积为( )| A. | ($\sqrt{2}$+1)π | B. | ($\sqrt{2}$+2)π | C. | ($\sqrt{2}$+3)π | D. | ($\sqrt{2}$+4)π |
20.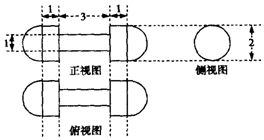 某几何体由三个圆柱和大小相同的两个半球组成,它的三视图如图所示(单位:dm),则该几何体的表面积是( )(侧视图中间有小圆)
某几何体由三个圆柱和大小相同的两个半球组成,它的三视图如图所示(单位:dm),则该几何体的表面积是( )(侧视图中间有小圆)
 某几何体由三个圆柱和大小相同的两个半球组成,它的三视图如图所示(单位:dm),则该几何体的表面积是( )(侧视图中间有小圆)
某几何体由三个圆柱和大小相同的两个半球组成,它的三视图如图所示(单位:dm),则该几何体的表面积是( )(侧视图中间有小圆)| A. | $\frac{25π}{2}$dm2 | B. | 11πdm2 | C. | $\frac{19π}{2}$dm2 | D. | 9πdm2 |