题目内容
9.在△ABC中,已知sinB=cosAsinC(1)判断△ABC的形状
(2)若$\overrightarrow{AB}$•$\overrightarrow{AC}$=9,又△ABC的面积等于6.求△ABC的三边之长;
(3)在(2)的条件下,设P是△ABC(含边界)内一点,P到三边AB,BC,CA的距离分别为d1,d2,d3,求d1+d2+d3的取值范围.
分析 (1)由题意和三角形的知识可得cosC=0,可得C=90°,△ABC为直角三角形;
(2)由数量积的意义可得$\overrightarrow{AB}$•$\overrightarrow{AC}$=|$\overrightarrow{AC}$|2=9,可得AC=3,再由三角形的面积公式可得BC=4,由勾股定理可得AB=5;
(3)以C为原点,CA、CB所在直线分别为x、y轴建立直角坐标系,设P的坐标为(x,y),可得d1+d2+d3=$\frac{x+2y+12}{5}$,且$\left\{\begin{array}{l}{x≥0}\\{y≥0}\\{4x+3y-12≤0}\end{array}\right.$,令x+2y=m,由线性规划的知识可得.
解答 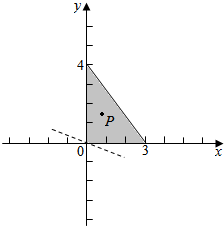 解:(1)∵在△ABC中sinB=cosAsinC,
解:(1)∵在△ABC中sinB=cosAsinC,
∴sin(A+C)=cosAsinC,
∴sinAcosC+cosAsinC=cosAsinC,
∴sinAcosC=0,即cosC=0,C=90°,
∴△ABC为直角三角形;
(2)∵$\overrightarrow{AB}$•$\overrightarrow{AC}$=|$\overrightarrow{AC}$|2=9,解得AC=3,
又ABC的面积S=$\frac{1}{2}$×3×BC=6,∴BC=4,
由勾股定理可得AB=5;
(3)以C为原点,CA、CB所在直线分别为x、y轴建立直角坐标系,
则A(3,0),B(0,4),可得直线AB的方程为$\frac{x}{3}$+$\frac{y}{4}$=1,即4x+3y-12=0,
设P的坐标为(x,y),则d1+d2+d3=x+y+$\frac{|4x+3y-12|}{\sqrt{{4}^{2}+{3}^{2}}}$,且$\left\{\begin{array}{l}{x≥0}\\{y≥0}\\{4x+3y-12≤0}\end{array}\right.$,
∴d1+d2+d3=x+y-$\frac{4x+3y-12}{5}$=$\frac{x+2y+12}{5}$,
令x+2y=m,由线性规划的知识可知0≤m≤8
∴d1+d2+d3的取值范围为[$\frac{12}{5}$,4]
点评 本题考查解三角形,涉及向量的知识和简单线性规划,数形结合是解决问题的关键,属中档题.

 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案| A. | $\frac{3\sqrt{3}}{4}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | $\frac{\sqrt{3}}{4}$ | D. | $\frac{\sqrt{3}}{12}$ |
| A. | x2+(y+2)2=5 | B. | x2+(y-2)2=5 | C. | (x-2)2+y2=5 | D. | (x-2)2+(y-2)2=5 |
| A. | 20 | B. | $4+2\sqrt{5}$ | C. | $4\sqrt{5}$ | D. | $8\sqrt{5}$ |
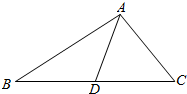 在△ABC中,D是BC中点,已知∠BAD+∠C=90°.
在△ABC中,D是BC中点,已知∠BAD+∠C=90°.