题目内容
20．求证：$\frac{\frac{1}{cos（-α）}+cos（180°+α）}{\frac{1}{sin（540°-α）}+sin（360°-α）}$=tan3α分析 已知等式左边利用诱导公式、同角三角函数间的基本关系化简得到结果与右边相等，即可得证．
解答 证明：等式左边=$\frac{\frac{1}{cosα}-cosα}{\frac{1}{sinα}-sinα}$=$\frac{\frac{1-co{s}^{2}α}{cosα}}{\frac{1-si{n}^{2}α}{sinα}}$=$\frac{si{n}^{2}α}{cosα}$×$\frac{sinα}{co{s}^{2}α}$=tan2α=右边．
得证．
点评 此题考查了诱导公式，同角三角函数间的基本关系的应用，熟练掌握公式是解本题的关键，属于基础题．
练习册系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
10．为研究质量x（单位：g）对弹簧长度y（单位：cm）的影响，对不同质量的6个物体进行测量，数据如下表所示：
（1）作出散点图，并求出线性回归方程；
（2）求出R2；
（3）进行残差分析．
| x/g | 5 | 10 | 15 | 20 | 25 | 30 |
| y/g | 7.25 | 8.12 | 8.95 | 9.90 | 10.9 | 11.8 |
（2）求出R2；
（3）进行残差分析．
11．设函数f（x）=xex-ax+a，若存在唯一的整数x0，使得f（x0）＜0，则实数a的取值范围是（ ）
| A． | [-$\frac{2}{3{e}^{2}}$，$\frac{1}{2e}$） | B． | [$\frac{2}{3{e}^{2}}$，$\frac{1}{2e}$） | C． | [-$\frac{1}{{e}^{2}}$，$\frac{1}{e}$） | D． | [$\frac{1}{{e}^{2}}$，$\frac{1}{e}$） |
15．数列{an}满足an-an+1=anan+1（n∈N*），数列{bn}满足bn=$\frac{1}{{a}_{n}}$，且b1+b2+…+b9=90，则b4•b6（ ）
| A． | 最大值为99 | B． | 为定值99 | C． | 最大值为100 | D． | 最大值为200 |
5．若sinx=$\frac{3-2m}{2}$，x∈[-$\frac{π}{6}$，$\frac{5π}{6}$]，则m的取值范围是（ ）
| A． | 1≤m≤2 | B． | $\frac{1}{2}$≤m≤2 | C． | -$\frac{1}{2}$≤m≤2 | D． | -2≤m≤1 |
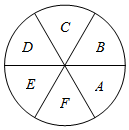如图所示，6个扇形区域A，B，C，D，E，F，现给这6个区域着色，要求同一个区域涂同一种颜色，相邻的两个区城不得使用同一种颜色，现有4种不同的颜色可用，那么一共有多少种不同的涂色方法？