题目内容

1．如图，圆x2+y2=8内有一点P（-1，2），AB为过点P的弦．
（1）当弦AB的倾斜角为135°时，求AB所在的直线方程及|AB|；
（2）当弦AB被点P平分时，写出直线AB的方程．

分析 （1）由倾斜角可得斜率为-1，然后根据过点P，写成点斜式，然后化成一般式即可．先求出圆心到直线AB的距离d，然后根据|AB|=$2\sqrt{{r^2}-{d^2}}$求值即可．
（2）根据OP⊥AB可求出AB的斜率，然后根据过点P，写出点斜式，转化为一般式方程即可．

解答 解：（1）依题意直线AB的斜率为-1，直线AB的方程为：y-2=-（x+1），即x+y-1=0；
圆心0（0，0）到直线AB的距离为d=$\frac{\sqrt{2}}{2}$，∴|AB|=2$\sqrt{8-\frac{1}{2}}$=$\sqrt{30}$；
（2）当弦AB被点P平分时，OP⊥AB，故AB的斜率为$\frac{1}{2}$，根据点斜式方程直线AB的方程为x-2y+5=0．

点评 本题考查用点斜式求直线方程，点到直线的距离公式，弦长公式的应用，求出圆心0（0，0）到直线AB的距离为d，是解题的关键．

练习册系列答案
相关题目
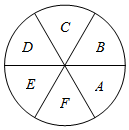9．如图所示，6个扇形区域A，B，C，D，E，F，现给这6个区域着色，要求同一个区域涂同一种颜色，相邻的两个区城不得使用同一种颜色，现有4种不同的颜色可用，那么一共有多少种不同的涂色方法？
12．（普通中学做）已知椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$（a＞b＞0）的离心率为$\frac{\sqrt{6}}{3}$，过右焦点F的直线l与C
相交于A、B两点，当l的斜率为1时，坐标原点O到l的距离为2．
（1）求椭圆C的方程；
（2）椭圆C上是否存在一点P，使得当l绕F转到某一位置时，有$\overrightarrow{OP}$=$\overrightarrow{OA}$+$\overrightarrow{OB}$成立？若存在，求点P的坐标与直线l的方程；若不存在，说明理由．
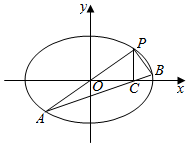9．如图，过坐标原点O的直线椭圆Г：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）于P，A两点，其中P在第一象限，B在椭圆Г上，直线AB与x轴交于点C．
（1）若椭圆Г的焦距为2$\sqrt{2}$，点P坐标为（$\sqrt{2}$，1），求椭圆Г的标准方程；
（2）求证：kBP•kBA=-$\frac{{b}^{2}}{{a}^{2}}$；
（3）若BP⊥AP，PC⊥x轴，求椭圆Г的离心率．
16．设命题p：x2-4ax+3a2＜0（其中a＞0，x∈R），命题q：-x2+5x-6≥0，x∈R．
（1）若a=1，且p∧q为真，求实数x的取值范围；
（2）若￢p是￢q的充分不必要条件，求实数a的取值范围．
6．等差数列{an}的前n项和为Sn，若S3=6，a1=4，则S5等于（　　）
A．-2B．0C．5D．10
13．已知椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1（a＞b＞0）$，焦点在直线x-2y-2=0上，且离心率为$\frac{1}{2}$．
（1）求椭圆方程；
 （2）过P（3，1）作直线l与椭圆交于A，B两点，P为线段AB的中点，求直线l的方程．
10．复数$\frac{5}{i-2}$等于（　　）
A．2-iB．-2-iC．2+iD．-2+i
11．椭圆C的中心在坐标原点，焦点在x轴上，焦点到短轴端点的距离为2，离心率为$\frac{\sqrt{3}}{2}$．
（Ⅰ）求该椭圆的方程；
（Ⅱ）若直线l与椭圆C交于A，B两点且OA⊥OB，是否存在以原点O为圆心的定圆与直线l相切？若存在求出定圆方程；若不存在，请说明理由．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网