题目内容
1.已知二次函数f(x)=ax2+bx+c(a,b,c∈R)对任意实数x,都有f(x)≥x,且当x∈[1,3)时,有$f(x)≤\frac{1}{8}{(x+2)^2}$成立.(1)证明:f(2)=2;
(2)若f(-2)=0,求f(x)的表达式;
(3)在题(2)的条件下设g(x)=f(x)-$\frac{mx}{2}$,x∈[0,+∞),若g(x)图象上的点都位于直线y=$\frac{1}{4}$的上方,求实数m的取值范围.
分析 (1)令x=2,求得f(2)≥2,且f(2)≤2,即可得证;
(2)由f(-2)=0,f(2)=2,求得b=$\frac{1}{2}$,4a+c=1即c=1-4a,再由二次不等式恒成立的条件为a>0,判别式非正,即可得到a,c,进而得到解析式;
(3)g(x)=f(x)-$\frac{mx}{2}$=$\frac{1}{8}$(x+2)2-$\frac{mx}{2}$,讨论x=0,x>0,不等式恒成立,注意运用参数分离和基本不等式求得最小值,即可得到m的范围.
解答 解:(1)证明:由题意可得f(2)≥2,且f(2)≤$\frac{1}{8}$(2+2)2=2,
即有f(2)=2;
(2)由f(-2)=0,可得4a-2b+c=0,
f(2)=2,即为4a+2b+c=2,
两式相减可得,b=$\frac{1}{2}$,4a+c=1即c=1-4a,
f(x)=ax2+$\frac{1}{2}$x+1-4a,
对任意实数x,都有f(x)≥x,即为
ax2-$\frac{1}{2}$x+1-4a≥0恒成立,即有a>0,△=$\frac{1}{4}$-4a(1-4a)≤0,
即有(8a-1)2≤0,即有a=$\frac{1}{8}$,c=$\frac{1}{2}$,
则f(x)=$\frac{1}{8}$x2+$\frac{1}{2}$x+$\frac{1}{2}$;
(3)g(x)=f(x)-$\frac{mx}{2}$=$\frac{1}{8}$(x+2)2-$\frac{mx}{2}$,
当x=0时,g(0)=$\frac{1}{2}$>$\frac{1}{4}$成立;
当x>0时,$\frac{1}{8}$(x+2)2-$\frac{mx}{2}$>$\frac{1}{4}$,
即有4m<$\frac{{x}^{2}+4x+2}{x}$=x+$\frac{2}{x}$+4,
由x+$\frac{2}{x}$≥2$\sqrt{x•\frac{2}{x}}$=2$\sqrt{2}$,当且仅当x=$\sqrt{2}$时,取得最小值.
即有4m<2$\sqrt{2}$+4,
解得m<1+$\frac{\sqrt{2}}{2}$.
综上可得,m的范围是(-∞,1+$\frac{\sqrt{2}}{2}$).
点评 本题考查二次函数的解析式的求法,注意运用二次不等式恒成立的条件,同时考查不等式恒成立的解法,注意运用参数分离和基本不等式,属于中档题.

| A. | [-$\frac{2}{3{e}^{2}}$,$\frac{1}{2e}$) | B. | [$\frac{2}{3{e}^{2}}$,$\frac{1}{2e}$) | C. | [-$\frac{1}{{e}^{2}}$,$\frac{1}{e}$) | D. | [$\frac{1}{{e}^{2}}$,$\frac{1}{e}$) |
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
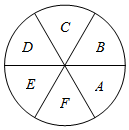 如图所示,6个扇形区域A,B,C,D,E,F,现给这6个区域着色,要求同一个区域涂同一种颜色,相邻的两个区城不得使用同一种颜色,现有4种不同的颜色可用,那么一共有多少种不同的涂色方法?
如图所示,6个扇形区域A,B,C,D,E,F,现给这6个区域着色,要求同一个区域涂同一种颜色,相邻的两个区城不得使用同一种颜色,现有4种不同的颜色可用,那么一共有多少种不同的涂色方法?