题目内容
8．某中学语文老师从《红楼梦》、《平凡的世界》、《红岩》、《老人与海》4本不同的名著中选出3本，分给三个同学去读，其中《红楼梦》为必读，则不同的分配方法共有（ ）| A． | 6种 | B． | 12种 | C． | 18种 | D． | 24种 |
分析 根据题意，分2步进行分析：①、先《平凡的世界》、《红岩》、《老人与海》三本书中选出2本，②、将选出的2本与《红楼梦》全排列，对应分给三个同学，求出每一步的情况数目，由分类计数原理计算可得答案．
解答 解：根据题意，分2步进行分析：
①、先《平凡的世界》、《红岩》、《老人与海》三本书中选出2本，有C32=3种选法，
②、将选出的2本与《红楼梦》全排列，对应分给三个同学，有A33=6种情况，
则不同的分配方法共有3×6=18种；
故选：C．
点评 本题考查排列、组合的综合应用，注意《红楼梦》为必读，是受到限制的元素，要优先分析．
练习册系列答案
名校联盟冲刺卷系列答案
名校提分一卷通系列答案
课程达标测试卷闯关100分系列答案
相关题目
19．某经销商从外地一水殖厂购进一批小龙虾，并随机抽取40只进行统计，按重量分类统计结果如下图：
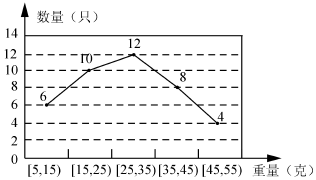
（1）记事件A为：“从这批小龙虾中任取一只，重量不超过35g的小龙虾”，求P（A）的估计值；
（2）试估计这批小龙虾的平均重量；
（3）为适应市场需求，制定促销策略．该经销商又将这批小龙虾分成三个等级，并制定出销售单价，如下表：
试估算该经销商以每千克至多花多少元（取整数）收购这批小龙虾，才能获得利润？
（1）记事件A为：“从这批小龙虾中任取一只，重量不超过35g的小龙虾”，求P（A）的估计值；
（2）试估计这批小龙虾的平均重量；
（3）为适应市场需求，制定促销策略．该经销商又将这批小龙虾分成三个等级，并制定出销售单价，如下表：
| 等级 | 一等品 | 二等品 | 三等品 |
| 重量（g） | [5，25） | [25，35） | [35，55] |
| 单价（元/只） | 1.2 | 1.5 | 1.8 |
3．
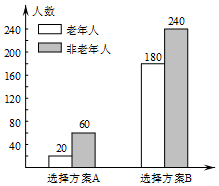为丰富人民群众业余生活，某市拟建设一座江滨公园，通过专家评审筛选出建设方案A和B向社会公开征集意见．有关部门用简单随机抽样方法调查了500名市民对这两种方案的看法，结果用条形图表示如下：
（Ⅰ）根据已知条件完成下面的2×2列联表，并用独立性检验的方法分析，能否在犯错误的概率不超过0.01的前提下认为是否选择方案A和年龄段有关？
附：
（Ⅱ）根据（Ⅰ）的结论，能否提出一个更好的调查方法，使得调查结果更具代表性，说明理由．
${K^2}=\frac{{n{{（ad-bc）}^2}}}{（a+b）（c+d）（a+c）（b+d）}$．
为丰富人民群众业余生活，某市拟建设一座江滨公园，通过专家评审筛选出建设方案A和B向社会公开征集意见．有关部门用简单随机抽样方法调查了500名市民对这两种方案的看法，结果用条形图表示如下：（Ⅰ）根据已知条件完成下面的2×2列联表，并用独立性检验的方法分析，能否在犯错误的概率不超过0.01的前提下认为是否选择方案A和年龄段有关？
| 选择方案A | 选择方案B | 总计 | |
| 老年人 | |||
| 非老年人 | |||
| 总计 | 500 |
（Ⅱ）根据（Ⅰ）的结论，能否提出一个更好的调查方法，使得调查结果更具代表性，说明理由．
| P（K2≥k） | 0.100 | 0.050 | 0.010 | 0.001 |
| k | 2.706 | 3.841 | 6.635 | 10.828 |
13．已知数列{an}是等差数列，其前n项和Sn有最大值，且$\frac{{{a_{2017}}}}{{{a_{2016}}}}$＜-1，则使得Sn＞0的n的最大值为（ ）
| A． | 2016 | B． | 2017 | C． | 4031 | D． | 4033 |