题目内容
2.已知x∈(-$\frac{π}{2}$,0),tanx=-$\frac{4}{3}$,则sin(x+π)等于( )| A. | $\frac{3}{5}$ | B. | -$\frac{3}{5}$ | C. | -$\frac{4}{5}$ | D. | $\frac{4}{5}$ |
分析 根据x的取值范围,tanx的值易得sinx=-$\frac{4}{5}$,所以结合诱导公式求得sin(x+π)的值即可.
解答 解:因为x∈(-$\frac{π}{2}$,0),tanx=-$\frac{4}{3}$,
所以sinx=-$\frac{4}{5}$,
∴sin(x+π)=-sinx=$\frac{4}{5}$.
故选:D.
点评 本题主要考察了同角三角函数关系式和诱导公式的应用,属于基本知识的考查.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
12.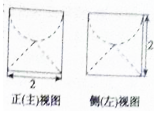 若某圆柱体的上部挖掉一个半球,下部挖掉一个圆锥后所得的几何体的三视图中的正(主)视图和侧(左)视图如图所示,则此几何体的表面积是( )
若某圆柱体的上部挖掉一个半球,下部挖掉一个圆锥后所得的几何体的三视图中的正(主)视图和侧(左)视图如图所示,则此几何体的表面积是( )
 若某圆柱体的上部挖掉一个半球,下部挖掉一个圆锥后所得的几何体的三视图中的正(主)视图和侧(左)视图如图所示,则此几何体的表面积是( )
若某圆柱体的上部挖掉一个半球,下部挖掉一个圆锥后所得的几何体的三视图中的正(主)视图和侧(左)视图如图所示,则此几何体的表面积是( )| A. | (4+$\sqrt{2}$)π | B. | 6$π+2\sqrt{2}π$ | C. | 6$π+\sqrt{2}π$ | D. | (8+$\sqrt{2}$)π |
11.F是椭圆C:$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1的右焦点,P为C上一动点,点A坐标为(1,1),则|PA|+|PF|的最小值为( )
| A. | 4+$\sqrt{5}$ | B. | 4-$\sqrt{5}$ | C. | 2 | D. | $\sqrt{5}$ |
12.当命题“若p则q”为真时,下列命题中一定正确的是( )
| A. | 若q则p | B. | 若¬p则¬q | C. | 若¬q则¬p | D. | p且q |