题目内容
20.在10L水中有3个细菌,从中任取4L水,设其中含有细菌的个数为X,求:(1)P(X=1);
(2)X的概率分布;
(3)E(X),D(X).(注:结果都用小数表示)
分析 (1)每个细菌被取的概率均为$\frac{2}{5}$,三个细菌独立,由此能求出P(x=1).
(2)由题意X~B(3,$\frac{2}{5}$),由此能求出X的概率分布列.
(3)由X~B(3,$\frac{2}{5}$),利用二项分布的性质能求出E(X),D(X).
解答 解:(1)∵在10L水中有3个细菌,从中任取4L水,
∴每个细菌被取的概率均为$\frac{2}{5}$,三个细菌独立,
∴P(x=1)=${C}_{3}^{1}(\frac{2}{5})(\frac{3}{5})^{2}$=$\frac{54}{125}$.
(2)由题意X~B(3,$\frac{2}{5}$),
P(X=0)=${C}_{3}^{0}(\frac{2}{5})^{0}(\frac{3}{5})^{3}$=$\frac{27}{125}$,
P(x=1)=${C}_{3}^{1}(\frac{2}{5})(\frac{3}{5})^{2}$=$\frac{54}{125}$.
P(X=2)=${C}_{3}^{2}(\frac{2}{5})^{2}(\frac{3}{5})$=$\frac{36}{125}$,
P(X=3)=${C}_{3}^{3}(\frac{2}{5})^{3}$=$\frac{8}{125}$,
∴X的概率分布列为:
| X | 0 | 1 | 2 | 3 |
| P | $\frac{27}{125}$ | $\frac{54}{125}$ | $\frac{36}{125}$ | $\frac{8}{125}$ |
∴E(X)=3×$\frac{2}{5}$=$\frac{6}{5}$,
D(X)=3×$\frac{2}{5}×\frac{3}{5}$=$\frac{18}{25}$.
点评 本题考查概率的求法,考查离散型随机变量的分布列和数学期望的求法,是中档题,解题时要认真审题,注意二项分布的性质的合理运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
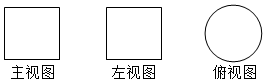 加图所示,一个空间几何体的主视图和左视图都是边长为3的正方形,俯视图是一个直径为3的圆,那么这个几何体的全面积为36π.
加图所示,一个空间几何体的主视图和左视图都是边长为3的正方形,俯视图是一个直径为3的圆,那么这个几何体的全面积为36π.
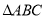 中,
中,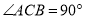 ,
,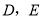 分别为
分别为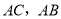 的中点,
的中点,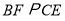 交
交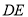 的延长线于点
的延长线于点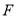 .
.
 是平行四边形;
是平行四边形; 时,求证:四边形
时,求证:四边形