题目内容
3.已知圆C的圆心是直线x-y+1=0与x轴的交点,且圆C与直线x+y+3=0相切.(I)求圆C的方程;
(Ⅱ)过点P(0,1)作倾斜角互补的两条直线,分别与圆C相交A、B两点.试判断直线AB的斜率是否为定值,并说明理由.
分析 (I)求出直线x-y+1=0与x轴的交点即为圆心C坐标,求出点C到直线x+y+3=0的距离即为圆的半径,写出圆的标准方程即可.
(Ⅱ)求出A,B的坐标,利用斜率公式,即可得出结论.
解答 解:(I)对于直线x-y+1=0,令y=0,得到x=-1,即圆心C(-1,0),
∵圆心C(-1,0)到直线x+y+3=0的距离d=$\frac{|-1+0+3|}{\sqrt{2}}$=$\sqrt{2}$,
∴圆C半径r=$\sqrt{2}$,
则圆C方程为(x+1)2+y2=2;
(Ⅱ)设A(x1,y1),B(x2,y2),设PA的方程为y=kx+1,
代入(x+1)2+y2=2化简得:(k2+1)x2+(2+2k)x=0,
∴x1=-$\frac{2+2k}{{k}^{2}+1}$,
用-k代替x1,y1中的k,得x2=-$\frac{2-2k}{{k}^{2}+1}$,
∴直线AB的斜率k=$\frac{{y}_{2}-{y}_{1}}{{x}_{2}-{x}_{1}}$=$\frac{-k({x}_{1}+{x}_{2})}{{x}_{2}-{x}_{1}}$=1为定值.
点评 此题考查了圆的标准方程,涉及的知识有:一次函数与x轴的交点,点到直线的距离公式,以及直线与圆的位置关系,求出圆心坐标与半径是解本题的关键.

练习册系列答案
相关题目
18.已知点P在△ABC内(不含边界),且$\overrightarrow{AP}$=x$\overrightarrow{AB}$+y$\overrightarrow{AC}$,则$\frac{y+1}{x+2}$的取值范围为( )
| A. | ($\frac{1}{3}$,1) | B. | ($\frac{1}{2}$,1) | C. | ($\frac{2}{3}$,1) | D. | ($\frac{1}{2}$,$\frac{2}{3}$) |
10.已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左、右焦点分别为F1、F2,P是直线x=a上一点,且PF1⊥PF2,|PF1|+|PF2|=2$\sqrt{2}$a,则双曲线的离心率是( )
| A. | $\sqrt{2}$ | B. | $\frac{2\sqrt{3}}{3}$ | C. | 2 | D. | $\sqrt{3}$ |
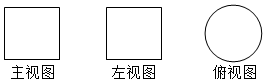 加图所示,一个空间几何体的主视图和左视图都是边长为3的正方形,俯视图是一个直径为3的圆,那么这个几何体的全面积为36π.
加图所示,一个空间几何体的主视图和左视图都是边长为3的正方形,俯视图是一个直径为3的圆,那么这个几何体的全面积为36π.