题目内容
15.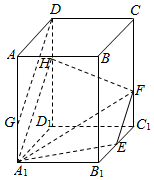 在正四棱柱ABCD-A1B1C1D1中,AB=2,AA1=3,E为B1C1的中点,F在CC1上,且C1F=1,G在AA1上,且AG=2.
在正四棱柱ABCD-A1B1C1D1中,AB=2,AA1=3,E为B1C1的中点,F在CC1上,且C1F=1,G在AA1上,且AG=2.(1)证明:DG∥平面A1EF;
(2)设平面A1EF与DD1交于点H,求线段DH的长,并求出截面A1EFH的面积.
分析 (1)构造四边形GMCD是平行四边形,利用线线平行,证明线面平行,从而证明DG∥平面A1EF;
(2)根据线面平行的性质定理,结合题意,得出截面A1EFH是等腰梯形,结合图中数据求出截面面积.
解答  解:(1)证明:如图所示,
解:(1)证明:如图所示,
设M为BB1上一点,且BM=2,连接MG、MC,易得GM∥DC,且GM=DC,
∴四边形GMCD是平行四边形,
∴DG∥CM;
在矩形B1C1CB中,C1E=C1F=1,BC=BM=2,
∴∠MCF=∠EFC=45°,∴FE∥CM,∴DG∥FE;
又DG?平面A1EF,FE?平面A1EF,
∴DG∥平面A1EF;
(2)∵DG∥平面A1EF,DG?平面AA1D1D,
平面AA1D1D∩平面A1EF=A1H,
∴DG∥A1H,∴DH=A1G=1;
由上易得截面A1EFH是等腰梯形;
其中EF=$\sqrt{2}$,A1H=2$\sqrt{2}$,A1E=$\sqrt{5}$;
由此可得等腰梯形A1EFH的高为$\frac{3\sqrt{2}}{2}$;
∴截面A1EFH的面积为$\frac{9}{2}$.
点评 本题考查了空间中的线线与线面平行的应用问题,也考查了空间想象能力与逻辑思维能力的应用问题,是综合性题目.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
3.已知圆C:(x+c)2+y2=4a2,点A(c,0),其中c>a>0,M是圆C上的动点,MA的中垂线交MC所在直线于P,则点P的轨迹是( )
| A. | 椭圆 | B. | 双曲线 | C. | 抛物线 | D. | 直线 |
4.函数f(x)=sin(x+$\frac{π}{6}$)-$\sqrt{3}$sin($\frac{π}{3}$-x)(x∈R)的最大值为( )
| A. | 1+$\sqrt{3}$ | B. | 2 | C. | 1 | D. | -1+$\sqrt{3}$ |
5.设集合A={x|x2-4<0},B={1,2,3},则A∩B=( )
| A. | {1,2,3} | B. | {1,2} | C. | {1} | D. | {2} |