题目内容
4.函数f(x)=sin(x+$\frac{π}{6}$)-$\sqrt{3}$sin($\frac{π}{3}$-x)(x∈R)的最大值为( )| A. | 1+$\sqrt{3}$ | B. | 2 | C. | 1 | D. | -1+$\sqrt{3}$ |
分析 由三角函数公式化简可得f(x)=2cos(x-$\frac{2π}{3}$),可得最大值为2
解答 解:f(x)=sin(x+$\frac{π}{6}$)-$\sqrt{3}$sin($\frac{π}{3}$-x)
=sin[$\frac{π}{2}$-($\frac{π}{3}$-x)]-$\sqrt{3}$sin($\frac{π}{3}$-x)
=cos($\frac{π}{3}$-x)-$\sqrt{3}$sin($\frac{π}{3}$-x)
=2cos($\frac{π}{3}$-x+$\frac{π}{3}$)=2cos(x-$\frac{2π}{3}$),
∴函数的最大值为2,
故选:B.
点评 本题考查三角函数恒等变换,涉及三角函数的最值,属基础题.

练习册系列答案
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案
相关题目
12. 定义在R上的可导函数f(x)的导函数为f′(x),已知函数y=2f′(x)的图象如图所示,则函数y=f(x)的单调递减区间为( )
定义在R上的可导函数f(x)的导函数为f′(x),已知函数y=2f′(x)的图象如图所示,则函数y=f(x)的单调递减区间为( )
 定义在R上的可导函数f(x)的导函数为f′(x),已知函数y=2f′(x)的图象如图所示,则函数y=f(x)的单调递减区间为( )
定义在R上的可导函数f(x)的导函数为f′(x),已知函数y=2f′(x)的图象如图所示,则函数y=f(x)的单调递减区间为( )| A. | (1,+∞) | B. | (1,2) | C. | (-∞,2) | D. | (2,+∞) |
9.已知圆C:x2+(y-4)2=100,点A为圆C上的动点,点B的坐标为(0,-4),动点P满足$\overrightarrow{CP}$=$λ\overrightarrow{PA}$(λ>0),($\overrightarrow{OA}$+$\overrightarrow{OB}$-2$\overrightarrow{OP}$)•($\overrightarrow{OA}$-$\overrightarrow{OB}$)=0,则点P的轨迹方程为( )
| A. | $\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{16}$=1 | B. | $\frac{{x}^{2}}{16}$+$\frac{{y}^{2}}{25}$=1 | C. | $\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{9}$=1 | D. | $\frac{{x}^{2}}{9}$+$\frac{{y}^{2}}{25}$=1 |
16.把函数y=sin(6x+$\frac{π}{6}$)图象上各点的横坐标扩大到原来的3倍(纵坐标不变),再将图象向右平移$\frac{π}{3}$个单位,那么所得函数图象的一条对称轴方程为( )
| A. | x=-$\frac{π}{2}$ | B. | x=-$\frac{π}{4}$ | C. | x=$\frac{π}{8}$ | D. | x=$\frac{π}{4}$ |
14.用数字0,1,2,3,4,5可以组成没有重复数字,并且比20000大的五位奇数共有( )
| A. | 288个 | B. | 144个 | C. | 240个 | D. | 126个 |
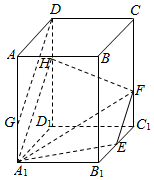 在正四棱柱ABCD-A1B1C1D1中,AB=2,AA1=3,E为B1C1的中点,F在CC1上,且C1F=1,G在AA1上,且AG=2.
在正四棱柱ABCD-A1B1C1D1中,AB=2,AA1=3,E为B1C1的中点,F在CC1上,且C1F=1,G在AA1上,且AG=2.