题目内容
10.与正方体各棱都相切的球称为棱切球,则它的体积与正方体体积之比为$\frac{\sqrt{2}}{3}π$.分析 由题意可得,棱切球的直径即为正方体的相对两条棱的距离,也就是正方体面上的对角线长,由此即可求得答案.
解答 解:设正方体的棱长为a,
由棱切球与正方体的各棱都相切,
可得棱切球的直径等于正方体的相对两条棱的距离,
故球的直径为正方体面上的对角线长:即2r=$\sqrt{2}a$,
则r=$\frac{\sqrt{2}}{2}a$,
∴棱切球的体积与正方体体积之比为$\frac{\frac{4}{3}π(\frac{\sqrt{2}}{2}a)^{3}}{{a}^{3}}=\frac{\sqrt{2}}{3}π$.
故答案为:$\frac{\sqrt{2}}{3}π$.
点评 本题是新定义题,考查了球的体积与正方体的体积,是基础题.

练习册系列答案
相关题目
4.(2x-$\frac{1}{2x}$)6的展开式的常数项( )
| A. | 20 | B. | -20 | C. | 40 | D. | -40 |
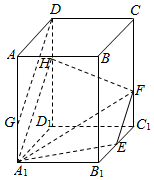 在正四棱柱ABCD-A1B1C1D1中,AB=2,AA1=3,E为B1C1的中点,F在CC1上,且C1F=1,G在AA1上,且AG=2.
在正四棱柱ABCD-A1B1C1D1中,AB=2,AA1=3,E为B1C1的中点,F在CC1上,且C1F=1,G在AA1上,且AG=2.