题目内容
7.梯形ABCD中,AB∥CD,AB=6,AD=DC=2,若$\overrightarrow{AD}$⊥$\overrightarrow{BC}$,则$\overrightarrow{AC}$•$\overrightarrow{BD}$=-12.分析 以AD所在直线为x轴,BC所在直线为y轴,建立直角坐标系,由平行线的性质定理可得OD=1,运用勾股定理进而得到OC,OD,求得A,B,C,D的坐标,由向量的数量积的坐标表示,计算即可得到.
解答 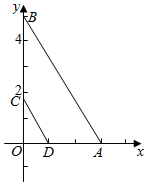 解:以AD所在直线为x轴,BC所在直线为y轴,建立直角坐标系,
解:以AD所在直线为x轴,BC所在直线为y轴,建立直角坐标系,
由AB∥CD可得,$\frac{OD}{OA}$=$\frac{CD}{BA}$,
即为$\frac{OD}{OD+2}$=$\frac{2}{6}$,解得OD=1,
可得OC=$\sqrt{4-1}$=$\sqrt{3}$,OB=$\sqrt{36-9}$=3$\sqrt{3}$,
即有A(3,0),D(1,0),B(0,3$\sqrt{3}$),C(0,$\sqrt{3}$),
则$\overrightarrow{AC}$•$\overrightarrow{BD}$=(-3,$\sqrt{3}$)•(1,-3$\sqrt{3}$)=-3•1+$\sqrt{3}$•(-3$\sqrt{3}$)=-12.
故答案为:-12.
点评 本题考查向量的数量积的求法,注意运用坐标法,同时考查向量的数量积的坐标表示,以及平行线的性质定理,考查运算能力,属于中档题.

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
相关题目
20.下列直线与圆(x-1)2+(y+2)2=5相切的是( )
| A. | 2x-y+1=0 | B. | 2x-y-1=0 | C. | 2x+y+1=0 | D. | 2x+y-1=0 |
12. 定义在R上的可导函数f(x)的导函数为f′(x),已知函数y=2f′(x)的图象如图所示,则函数y=f(x)的单调递减区间为( )
定义在R上的可导函数f(x)的导函数为f′(x),已知函数y=2f′(x)的图象如图所示,则函数y=f(x)的单调递减区间为( )
 定义在R上的可导函数f(x)的导函数为f′(x),已知函数y=2f′(x)的图象如图所示,则函数y=f(x)的单调递减区间为( )
定义在R上的可导函数f(x)的导函数为f′(x),已知函数y=2f′(x)的图象如图所示,则函数y=f(x)的单调递减区间为( )| A. | (1,+∞) | B. | (1,2) | C. | (-∞,2) | D. | (2,+∞) |
16.把函数y=sin(6x+$\frac{π}{6}$)图象上各点的横坐标扩大到原来的3倍(纵坐标不变),再将图象向右平移$\frac{π}{3}$个单位,那么所得函数图象的一条对称轴方程为( )
| A. | x=-$\frac{π}{2}$ | B. | x=-$\frac{π}{4}$ | C. | x=$\frac{π}{8}$ | D. | x=$\frac{π}{4}$ |
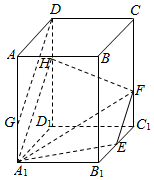 在正四棱柱ABCD-A1B1C1D1中,AB=2,AA1=3,E为B1C1的中点,F在CC1上,且C1F=1,G在AA1上,且AG=2.
在正四棱柱ABCD-A1B1C1D1中,AB=2,AA1=3,E为B1C1的中点,F在CC1上,且C1F=1,G在AA1上,且AG=2.