题目内容
命题“?x∈（0，+∞），x3-x2+1≥0，”的否定是（ ）
| A、?x∈（0，+∞），x3-x2+1≤0 |
| B、?x∈（0，+∞），x3-x2+1≤0 |
| C、?x∈（0，+∞），x3-x2+1＜0 |
| D、?x∈（0，-∞），x3-x2+1＜0 |
考点：命题的否定
专题：简易逻辑
分析：全称命题的否定是特称命题，写出结果即可．
解答：
解：全称命题的否定是特称命题，
命题“?x∈（0，+∞），x3-x2+1≥0，”的否定是?x∈（0，+∞），x3-x2+1＜0．
故选：C．
命题“?x∈（0，+∞），x3-x2+1≥0，”的否定是?x∈（0，+∞），x3-x2+1＜0．
故选：C．
点评：本题考查命题的否定，注意全称命题与特称命题的否定关系．
练习册系列答案
相关题目
一个正方体内接于一个球，过球心作一个截面，则截面不可能的图形为（ ）
A、 |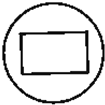
B、 |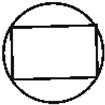
C、 |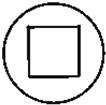
D、 |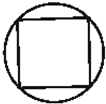
我们知道十进制数有10个数码即0～9，进位规则是“逢十进一”，如47+56=103；由此可知八进制数有8个数码即0～7，进位规则是“逢八进一”，则在八进制下做如下运算47+56=（ ）
| A、85 | B、103 |
| C、125 | D、185 |
在如图所示的茎叶图中，甲、乙两组数据的中位数分别是（ ）
| A、42 42 |
| B、45 46 |
| C、45 42 |
| D、47 48 |