题目内容
已知函数g(x)=2x-1,函数y=f(x)是y=g(x)的反函数,设a>b>c>0,则
,
,
的大小关系为( )
| f(a) |
| a |
| f(b) |
| b |
| f(c) |
| c |
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
考点:反函数
专题:函数的性质及应用
分析:先求出g(x)的反函数,然后通过去特值令a=15,b=7,c=1,判定出三个式子的大小.
解答:
解:∵g(x)=2x-1,
∴x=log2(y+1)
∴g(x)=2x-1的反函数为:f(x)=log2(x+1)
∵a>b>c>0,
∴取特值,令a=15,b=7,c=1,
∴则
=
=
,
=
=
,
=
=1
∵
<
<1
∴
<
<
故选B.
∴x=log2(y+1)
∴g(x)=2x-1的反函数为:f(x)=log2(x+1)
∵a>b>c>0,
∴取特值,令a=15,b=7,c=1,
∴则
| f(a) |
| a |
| log216 |
| 15 |
| 4 |
| 15 |
| f(b) |
| b |
| log28 |
| 7 |
| 3 |
| 7 |
| f(c) |
| c |
| log22 |
| 1 |
∵
| 4 |
| 15 |
| 3 |
| 7 |
∴
| f(a) |
| a |
| f(b) |
| b |
| f(c) |
| c |
故选B.
点评:本题考查反函数的求法,在解决选择题时,排除法是常用的一种方法.

练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
函数f(x)=
ln
的图象可能是( )
| 1 |
| 3 |
| 1+x |
| 1-x |
A、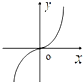 |
B、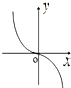 |
C、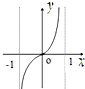 |
D、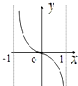 |
已知M={x∈R|x≥2
},a=π,有下列四个式子:①a∈M;②{a}?M;③a⊆M;④{a}∩M=π,其中正确的是( )
| 2 |
| A、①② | B、①④ | C、②③ | D、①②④ |
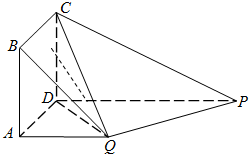 在如图所示的多面体中,四边形ABCD为正方形,四边形ADPQ是直角梯形,AD⊥DP,CD⊥平面ADPQ,AB=AQ=
在如图所示的多面体中,四边形ABCD为正方形,四边形ADPQ是直角梯形,AD⊥DP,CD⊥平面ADPQ,AB=AQ=| 1 |
| 2 |
(1)求证:PQ⊥平面DCQ;
(2)若AQ=2,求四面体C-BDQ的体积.
若U={1,2,3,4,5,6,7},A={3,4,6,7},B={3,5,6,7},则∁U(A∩B)=( )
| A、{1,2,4,5} |
| B、{2,6,8} |
| C、{1,3,5,7} |
| D、{1,2} |
若M⊆U,N⊆U,且M⊆N,则( )
| A、M∩N=N |
| B、M∪N=M |
| C、∁UN⊆∁UM |
| D、∁UM⊆∁UN |