题目内容
已知函数f(x)=mx2-2(3-m)x+4,g(x)=mx,若对于任一实数x,f(x)与g(x)至少有一个为正数,则实数m的取值范围是( )
| A、(0,3] |
| B、(0,9) |
| C、(1,9) |
| D、(-∞,9] |
考点:一元二次方程的根的分布与系数的关系
专题:计算题,分类讨论,函数的性质及应用,不等式的解法及应用
分析:由图象可判断m≤0时不合题意;当m>0时,x>0,g(x)>0成立,只需x≤0时,f(x)>0即可,分对称轴在y轴右侧、左侧两种情况讨论,借助图象可得不等式;
解答:
解:当m≤0时,由函数图象可知,不符合题意;
当m>0时,当x>0,g(x)>0成立,
∴只需x≤0时,f(x)>0即可,
,符合题意,解得0<m≤3;
若
,即有
,符合题意,解得3<m<9;
综上所述,0<m<9.
故选B.
当m>0时,当x>0,g(x)>0成立,
∴只需x≤0时,f(x)>0即可,
|
若
|
|
综上所述,0<m<9.
故选B.
点评:该题考查一次函数、二次函数的单调性,考查不等式的求解,考查分类讨论思想.

练习册系列答案
 天天练口算系列答案
天天练口算系列答案
相关题目
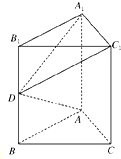 如图所示,在直三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,AB=AC=1,AA1=2,∠B1A1C1=90°,D为BB1中点,求证:AD⊥平面A1DC1.
如图所示,在直三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,AB=AC=1,AA1=2,∠B1A1C1=90°,D为BB1中点,求证:AD⊥平面A1DC1. 某几何体三视图如图所示,其中正视图和侧视图都是等腰梯形,且上底长为2,下底长为4,腰长为
某几何体三视图如图所示,其中正视图和侧视图都是等腰梯形,且上底长为2,下底长为4,腰长为