题目内容
19.已知曲线C的极坐标方程为2ρsinθ+ρcosθ=10.曲线 c1:$\left\{\begin{array}{l}{x=3cosα}\\{y=2sinα}\end{array}\right.$(α为参数).(Ⅰ)求曲线c1的普通方程;
(Ⅱ)若点M在曲线C1上运动,试求出M到曲线C的距离的最小值.
分析 (1)用x,y表示出cosα,sinα利用cos2α+sin2α=1消参数得到曲线C1的普通方程;
(2)先求出曲线C的普通方程,使用参数坐标求出点M到曲线C的距离,得到关于α的三角函数,利用三角函数的性质求出距离的最值.
解答 解:(Ⅰ)∵$\left\{\begin{array}{l}{x=3cosα}\\{y=2sinα}\end{array}\right.$,∴cosα=$\frac{x}{3}$,sinα=$\frac{y}{2}$,∴曲线C1的普通方程是:$\frac{x^2}{9}+\frac{y^2}{4}=1$.
(Ⅱ)曲线C的普通方程是:x+2y-10=0.
点M到曲线C的距离为$d=\frac{{|{3cosα+4sinα-10}|}}{{\sqrt{5}}}=\frac{1}{{\sqrt{5}}}|{5cos(α-φ)-10}|$,($cosφ=\frac{3}{5},sinφ=\frac{4}{5}$).
∴α-φ=0时,${d_{min}}=\sqrt{5}$,此时$M(\frac{9}{5},\frac{8}{5})$.
点评 本题考查了参数方程,极坐标方程与普通方程的转化,参数方程的应用,属于基础题.

练习册系列答案
相关题目
8. 如图,空间四边形OABC中,点M在OA上,且OM=2MA,点N为BC中点,$\overrightarrow{MN}=x\overrightarrow{OA}+y\overrightarrow{OB}+z\overrightarrow{OC}$,则x,y,z的值分别是( )
如图,空间四边形OABC中,点M在OA上,且OM=2MA,点N为BC中点,$\overrightarrow{MN}=x\overrightarrow{OA}+y\overrightarrow{OB}+z\overrightarrow{OC}$,则x,y,z的值分别是( )
 如图,空间四边形OABC中,点M在OA上,且OM=2MA,点N为BC中点,$\overrightarrow{MN}=x\overrightarrow{OA}+y\overrightarrow{OB}+z\overrightarrow{OC}$,则x,y,z的值分别是( )
如图,空间四边形OABC中,点M在OA上,且OM=2MA,点N为BC中点,$\overrightarrow{MN}=x\overrightarrow{OA}+y\overrightarrow{OB}+z\overrightarrow{OC}$,则x,y,z的值分别是( )| A. | $-\frac{2}{3},\frac{1}{2},\frac{1}{2}$ | B. | $\frac{1}{2},-\frac{2}{3},\frac{1}{2}$ | C. | $\frac{1}{2},\frac{1}{2},-\frac{1}{2}$ | D. | $\frac{2}{3},\frac{2}{3},-\frac{1}{2}$ |
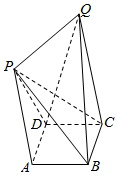 如图,在四棱锥P-ABCD中.底面ABCD为矩形,侧棱PA⊥平面ABCD,AP∥CQ,AB=2BC=2,CQ=$\frac{3}{2}$AP=3.
如图,在四棱锥P-ABCD中.底面ABCD为矩形,侧棱PA⊥平面ABCD,AP∥CQ,AB=2BC=2,CQ=$\frac{3}{2}$AP=3.