题目内容
在△ABC中，角A，B，C的对边分别为a，b，c，且
=-
．
（1）求角A的值；
（2）若
•
=-2，求|
|的最小值；
（3）若b=
，c=2m，O是△ABC的外心，且
=x
+y
，求x+y的最小值．
| 2b+c |
| a |
| cosC |
| cosA |
（1）求角A的值；
（2）若
| AB |
| AC |
| BC |
（3）若b=
| 2 |
| m |
| AO |
| AB |
| AC |
考点：正弦定理,平面向量数量积的运算
专题：解三角形
分析：（1）已知等式左边利用正弦定理化简，整理后求出cosA的值，即可确定出A的度数；
（2）利用平面向量的数量积运算法则化简已知等式，将cosA的值代入求出bc的值，再利用余弦定理列出关系式，并利用基本不等式变形，将bc的值代入即可求出所求式子的最小值；
（3）利用平面向量的数量积运算法则化简
•
，将b，c，cosA的值代入求出值，设AB的中点为D，则有OD⊥AB，即
•
=0，利用平面向量数量积运算法则表示出
•
，以及
•
，根据题意表示出x与y，利用基本不等式即可求出x+y的最小值．
（2）利用平面向量的数量积运算法则化简已知等式，将cosA的值代入求出bc的值，再利用余弦定理列出关系式，并利用基本不等式变形，将bc的值代入即可求出所求式子的最小值；
（3）利用平面向量的数量积运算法则化简
| AB |
| AC |
| DO |
| AB |
| AO |
| AB |
| AO |
| AC |
解答：
解：（1）由正弦定理得：
=
，
代入已知等式得：
=-
，
即2sinBcosA=-（sinAcosC+sinCcosA）=-sin（A+C）=-sinB，
∵sinB≠0，∴cosA=-
，
∵A为三角形内角，
∴A=
；
（2）由
•
=-2，得到bccosA=-2，
将cosA=-
代入得：bc=4，
由余弦定理得：|
|2=a2=b2+c2-2bccosA=b2+c2+bc，
∵b2+c2≥2bc，
∴|
|2≥3bc=12，即|
|≥2
，
则当b=c时，|
|的最小值为2
；
（3）∵
•
=|
|•|
|•cosA=2m•
•（-
）=-2，
设AB的中点为D，则有OD⊥AB，即
•
=0，
∴
•
=（
+
）•
=
•
+
•
=
•
=
2=2m2，
同理可得
•
=
2=
，
∴
，即
，
解得：
，
∴x+y=
+
=
+
（m2+
）≥
+
=2，
当且仅当m=1时，m2+
的最小值为2，
则x+y的最小值为2．
| 2b+c |
| a |
| 2sinB+sinC |
| sinA |
代入已知等式得：
| 2sinB+sinC |
| sinA |
| cosC |
| cosA |
即2sinBcosA=-（sinAcosC+sinCcosA）=-sin（A+C）=-sinB，
∵sinB≠0，∴cosA=-
| 1 |
| 2 |
∵A为三角形内角，
∴A=
| 2π |
| 3 |
（2）由
| AB |
| AC |
将cosA=-
| 1 |
| 2 |
由余弦定理得：|
| BC |
∵b2+c2≥2bc，
∴|
| BC |
| BC |
| 3 |
则当b=c时，|
| BC |
| 3 |
（3）∵
| AB |
| AC |
| AB |
| AC |
| 2 |
| m |
| 1 |
| 2 |
设AB的中点为D，则有OD⊥AB，即
| DO |
| AB |
∴
| AO |
| AB |
| AD |
| DO |
| AB |
| AD |
| AB |
| DO |
| AB |
| AD |
| AB |
| 1 |
| 2 |
| AB |
同理可得
| AO |
| AC |
| 1 |
| 2 |
| AC |
| 2 |
| m2 |
∴
|
|
解得：
|
∴x+y=
| 2m2+1 |
| 3m2 |
| m2+2 |
| 3 |
| 4 |
| 3 |
| 1 |
| 3 |
| 1 |
| m2 |
| 4 |
| 3 |
| 2 |
| 3 |
当且仅当m=1时，m2+
| 1 |
| m2 |
则x+y的最小值为2．
点评：此题考查了正弦定理，以及平面向量的数量积运算，熟练掌握正弦定理是解本题的关键．
练习册系列答案
相关题目
若集合M={1，2}，N={2，3，4，5}，则M∪N的元素有（ ）
| A、1个 | B、2个 | C、5个 | D、6个 |
如图，设四棱锥S-ACDE的底面为菱形，且∠ABC=60°，AB=SC=2，SA=SB=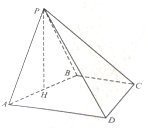
如图，四棱锥P-ABCD，底面ABCD为直角梯形，BC∥AD，BC⊥CD，BC=CD=
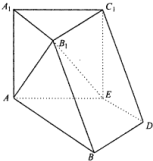如图，在六面体A1B1C1-ABDE中，平面A1B1C1∥平面ABDE，△A1B1C1是正三角形，四边形AA1B1B是直角梯形，AA1⊥AB，四边形AEC1A1是正方形，四边形ABDE是等腰梯形，AB∥DE，AB=2AE=2DE=2．