题目内容
设f(x)=
,则
f(x)dx等于( )
|
| ∫ | 2 0 |
A、
| ||
B、
| ||
C、
| ||
| D、不存在 |
考点:定积分
专题:导数的概念及应用
分析:原积分化为
f(x)dx=
x2dx+
(2-x)dx,根据定积分的计算法则计算即可
| ∫ | 2 0 |
| ∫ | 1 0 |
| ∫ | 2 1 |
解答:
解:
f(x)dx=
x2dx+
(2-x)dx=
x3|
+(2x-
x2)|
=
+(2×2-
×22)-(2-
)=
+4-2-2+
=
故选:C
| ∫ | 2 0 |
| ∫ | 1 0 |
| ∫ | 2 1 |
| 1 |
| 3 |
1 0 |
| 1 |
| 2 |
2 1 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
| 5 |
| 6 |
故选:C
点评:本题考查了定积分的计算,关键是求出原函数,属于基础题,

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
(1-
)5的展开式x2的系数是( )
| x |
| A、-5 | B、5 | C、-10 | D、10 |
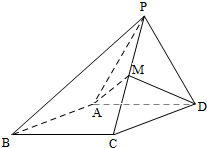 如图,四棱锥P-ABCD,侧面PAD是边长为2的正三角形,且与底面垂直,底面ABCD是∠ABC=60°的菱形,M为PC的中点.
如图,四棱锥P-ABCD,侧面PAD是边长为2的正三角形,且与底面垂直,底面ABCD是∠ABC=60°的菱形,M为PC的中点.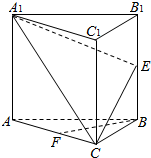 如图,在正三棱柱ABC-A1B1C1中,E,F分别为BB1,AC的中点.
如图,在正三棱柱ABC-A1B1C1中,E,F分别为BB1,AC的中点.