题目内容
已知a,b,c分别为△ABC的内角A,B,C所对的边,且acosC+ccosA=2bcosB,求:
(1) 角B的大小;
(2) sinA+sinC的取值范围.
(1) 方法一:由acos C+ccos A=2bcos B及余弦定理,得
a·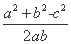 +c·
+c·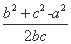 =2b·
=2b·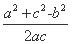 ,
,
化简,得a2+c2-b2=ac,
所以cos B=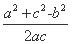 =
=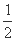 .
.
因为B∈(0,π),所以B= .
.
方法二:由acos C+ccos A=2bcos B及正弦定理,
得sin Acos C+sin Ccos A=2sin Bcos B,
即sin(A+C)=2sin Bcos B,
因为A+B+C=π,所以sin(A+C)=sin B≠0,
所以cos B=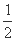 .
.
因为B∈(0,π),所以B= .
.
(2) sin A+sin C=sin A+sin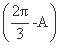 =
=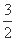 sin A+
sin A+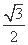 cos A=
cos A=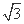 sin
sin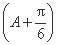 ,
,
因为0<A< ,所以
,所以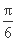 <A+
<A+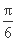 <
<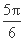 ,
,
所以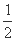 <sin
<sin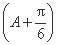 ≤1,
≤1,
所以sin A+sin C的取值范围是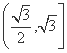 .
.

练习册系列答案
 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案
相关题目
 A1B1C1中,AB⊥AC,AB=2,AC=4,AA1=3,点D是BC的中点.
A1B1C1中,AB⊥AC,AB=2,AC=4,AA1=3,点D是BC的中点.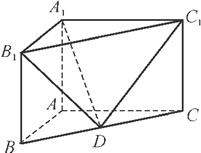
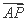 =
=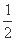 sin2θ·
sin2θ·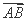 +cos2θ·
+cos2θ·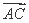 (θ∈R),则(
(θ∈R),则(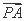 +
+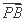 )·
)·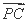 的最小值是 .
的最小值是 . 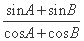 .
.


 为等差数列,若
为等差数列,若 <-1,且它们的前n项和Sn有最大值,则使得Sn>0的n的最大值为 .
<-1,且它们的前n项和Sn有最大值,则使得Sn>0的n的最大值为 .  +
+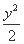 =1的焦点为F1,F2,点P在椭圆上,若PF1=4,则∠F1PF2的大小为 .
=1的焦点为F1,F2,点P在椭圆上,若PF1=4,则∠F1PF2的大小为 .