题目内容
9.已知向量$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$,$\overrightarrow{d}$及实数x,y满足|$\overrightarrow{a}$|=|$\overrightarrow{b}$|=1,$\overrightarrow{c}$=$\overrightarrow{a}$+(x2-3)$\overrightarrow{b}$,$\overrightarrow{d}$=-y•$\overrightarrow{a}$+x•$\overrightarrow{b}$,若$\overrightarrow{a}$⊥$\overrightarrow{b}$,$\overrightarrow{c}$⊥$\overrightarrow{d}$,且|$\overrightarrow{c}$|≤$\sqrt{10}$.(1)求y关于x的函数关系式y=f(x)及其定义域;
(2)若当x∈(1,$\sqrt{6}$)时,不等式f(x)≥mx+16恒成立,求实数m的取值范围.
分析 (1)由$\overrightarrow{c}•\overrightarrow{d}$=0整理得出f(x)的解析式,由|$\overrightarrow{c}$|≤$\sqrt{10}$列出不等式求出定义域;
(2)分别作出y=f(x)和y=mx+16的函数图象.根据图象关系得出m的范围.
解答 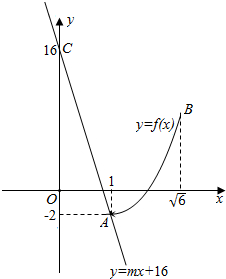 解:(1)∵$\overrightarrow{a}$⊥$\overrightarrow{b}$,∴$\overrightarrow{a}•\overrightarrow{b}$=0,∵$\overrightarrow{c}$⊥$\overrightarrow{d}$,∴$\overrightarrow{c}•\overrightarrow{d}$=0,∴[$\overrightarrow{a}$+(x2-3)$\overrightarrow{b}$]•(-y•$\overrightarrow{a}$+x•$\overrightarrow{b}$)=0,即-y$\overrightarrow{a}$2+x(x2-3)$\overrightarrow{b}$2=0,
解:(1)∵$\overrightarrow{a}$⊥$\overrightarrow{b}$,∴$\overrightarrow{a}•\overrightarrow{b}$=0,∵$\overrightarrow{c}$⊥$\overrightarrow{d}$,∴$\overrightarrow{c}•\overrightarrow{d}$=0,∴[$\overrightarrow{a}$+(x2-3)$\overrightarrow{b}$]•(-y•$\overrightarrow{a}$+x•$\overrightarrow{b}$)=0,即-y$\overrightarrow{a}$2+x(x2-3)$\overrightarrow{b}$2=0,
∵${\overrightarrow{a}}^{2}$=${\overrightarrow{b}}^{2}$=1,∴y=x(x2-3)=x3-3x.
∵|$\overrightarrow{c}$|≤$\sqrt{10}$,∴[$\overrightarrow{a}$+(x2-3)$\overrightarrow{b}$]2=1+(x2-3)2≤10,解得-$\sqrt{6}$≤x≤$\sqrt{6}$.
∴f(x)=x3-3x.定义域是[-$\sqrt{6}$,$\sqrt{6}$].
(2)f′(x)=3x2-3,∵x∈(1,$\sqrt{6}$),∴f′(x)>0,∴f(x)在(1,$\sqrt{6}$)上是增函数,
作出f(x)在(1,$\sqrt{6}$)上的函数图象如下:
令g(x)=mx+16,由图象可知当g(x)经过A(1,-2)时m取得最大值-18,
∴m≤-18.
点评 本题考查了平面向量的数量积运算,函数恒成立问题,借助函数图象可快速找到符合条件的m.

| A. | f(x)=0 | B. | f(x)=2 | C. | f(x)=x2-1 | D. | f(x)=x-$\frac{1}{x}$ |
| A. | -1<x<2 | B. | x<-1或x>2 | C. | x<-1或x>4 | D. | -4<x<8 | ||||
| E. | x<-4或x>8 |